정점 구를 적용하여 설계한 안경렌즈의 수차특성 분석



초록
정점 구를 원시 보정렌즈에 적용하여 설계하였다. 그리고 최적화 과정을 통하여 얻은 광학적 수차 특성과 그에 따른 스톱 위치를 찾아보고, 추후 원시 보정렌즈 설계 시 수차 특성 및 성능평가 비교 자료로 활용하는 데 있다.
+1.00 D원시안, +4.00 D원시안, +8.00 D원시안, 그리고 +11.00 D원시안 각각에 원시 보정렌즈 후면에 정점 구를 적용하여 초기설계를 하고, 이를 굴절성 원시 모델 안과 함께 최적화 과정을 통하여 최종 설계를 하였다, 그리고 정시 모델 안이 갖고 있는 광학적 수차특성과 비교하여 보고, 또한 스톱 위치를 알아보았다.
비점수차 그리고 왜곡수차를 정시 모델 안이 갖고 있는 수차와 비교한 결과, 중심시야와 주변시야 모두에서 정시 모델 안이 갖고 있는 수차보다 좋게 나타났다. 또한 최적화 과정을 통하여 얻은 최종 성능평가는 정시안의 공간 주파수 7 line pairs/mm에서 자오면과 구결면 모두에서 MTF(Modulation Transfer Function)값이 F = +1.00 D에서 약 30%, F = +4.00 D에서 약 50%, F = +8.00 D에서 약 62%, 그리고 F = +11.00 D에서 약 33% 정도의 값이 나왔다.
유효굴절력이 발생되지 않는 정점 구를 원시 보정렌즈에 적용하여 설계 하였다. 그리고 그 광학적 수차 특성을 정시 모델안의 광학적 수차 특성과 비교해 보았다. 뿐만 아니라 주변시야에서 보다 선명한 상을 얻기 위해서는, 원시 보정렌즈 설계 시 렌즈면의 만곡도를 좀 더 고려하여 설계해야 될 것으로 생각된다.
Abstract
Corrective lenses for hyperopia were designed using Vertex Sphere, and their optical aberration characteristics and stop positions were estimated through the optimization process. The aim of this study was to obtain indicators for the aberration characteristics and performance evaluation while designing corrective lenses for hyperopia.
In the initial design, Vertex Sphere was applied on the back surface of the corrective lens for hyperopia of powers of +1.00, +4.00, +8.00, and +11.00 D. The final design was obtained through the optimization process of this corrective lens for hyperopia in combination with a refractive ametropic eye model. The optical aberration characteristic of the schematic eye was compared, and the stop position was determined.
The aberrations were better in the eyes with astigmatism and distortion than in the schematic eye in both the central and peripheral visions. Furthermore, in the final performance evaluation obtained through the optimization process, the values of the modulation transfer function in both the tangential and sagittal planes at a spatial frequency of 7 line pairs/mm in the normal eyes were approximately 30%, 40%, 62%, and 33% at powers of +1.00, +4.00, +8.00, and +11.00 D, respectively.
Corrective lenses for hyperopia were designed using Vertex Sphere, which did not generate the effective refractive power, and their optical aberration characteristics were compared with those of the schematic eyes. To visualize clear images in the peripheral vision, higher curvatures of the lens surface should be considered when designing corrective lenses for hyperopia.
Keywords:
Hyperopia, Model eye, Astigmatism, Field of curvature, Distortion키워드:
원시안, 모델 안, 비점수차, 상면만곡수차, 왜곡수차서 론
오늘날 사용하고 있는 비정시 보정렌즈의 목적은 선명한 시야를 얻는데 있다. 선명한 시야를 얻기 위해서는 무엇보다도 광학적인 수차 보정이 이루어져야 한다. 초기 렌즈 형상은 양 볼록렌즈 혹은 양 오목렌즈이었지만 보정렌즈의 수차가 너무 커 평볼록렌즈 혹은 평오목렌즈의 형상으로 변화되었다. 그 후 더욱 선명한 시야를 얻기 위해 수차 보정 과정을 거치면서 1804년에는 지금의 보정렌즈 형상인 메니스커스 렌즈 형상을 갖게 되었다. 보정렌즈의 발전이 거듭되면서 원시, 근시 보정렌즈 뿐만 아니라, 난시보정용 렌즈가 1964년 초에 Univis 렌즈 회사에서 마이너스 토릭렌즈가 소개되었고, 1909년에는 Zeiss 광학회사에서 상업적으로 비구면 보정렌즈가 생산되었다.[1] 이 또한 보정렌즈의 광학적 수차를 줄이기 위해 사용된 렌즈의 형상 변화라 할 수 있다.
렌즈 설계 시 수차 보정을 위한 종류에는 색수차를 제외한 단색수차에 5가지 종류가 있다. 비정시 눈을 보정하기 위한 렌즈 설계 시 주로 비점수차와 상면만곡수차 제거에 중점을 두고 설계를 하고 있다. 그러나 비정시 보정용 렌즈 설계 시 비점수차와 상면만곡수차를 동시에 제거하기 어려워, 설계 시 주안점을 비점수차 제거에 먼저 두거나 아니면 비점수차를 남겨두고 상면만곡수차 제거에 주안점을 두고 설계하는 두 가지 설계 방식이 있는 것으로 알려져 있다. 이러한 설계 방식 중, 비점수차 제거 설계 방식으로 대표적인 방식은 Jalie에 의해 유도된 표현식에 의해 렌즈를 설계하는 것이다. 이 식에 의하면 두 가지 형태의 면 굴절력 값을 얻게 되는데, 하나는 렌즈 면의 만곡도가 심한 렌즈 형상으로 이를 Wollaston 형태라 하고, 다른 하나는 렌즈 면의 만곡도가 얕은 렌즈 형상으로 이를 Ostwallt 형태라 하고 있다. 1904년 M. Tscherning은 이를 –23.00 D에서 +7.25 D 굴절력 영역에서 작도를 하여 비점수차 제거에 대한 이론적인 토대를 마련하였는데, 이를 Tscherning`s ellipse로 불리워지고 있다.[1,2]
이러한 렌즈를 설계하는 경우, 이 들 수차를 제거하기 위해 안구 회전 중심점에 가상의 스톱이 있다고 생각하고 그 위치를 27 mm, FOV(Field of View) 30°내에서 주로 설계가 이루어 졌다. 또한 렌즈 면의 만곡도가 심한 Wollaston 형태보다 만곡도가 얕은 Ostwallt 형태가 현재 까지 주를 이루고 있다. 그러나 2000년대에 들어오면서 렌즈 면의 만곡도를 좀 더 심하게 하고, FOV 또한 주변시야 범위를 30°보다 좀 더 폭넓은 40°까지 고려하여 설계를 하여 특허를 낸 경우도 있다.[3]
본 논문에서는 이론적인 구인 정점 구(Vertex Sphere)의 곡률 반경을 실제 원시 보정렌즈 후면에 적용하여 설계하여 보았다. 정점 구는 시선 방향에 따라 보정렌즈의 유효굴절력이 발생되지 않는 렌즈 면의 곡률을 갖고 있어, 그 광학적 수차 특성과 성능 평가를 통해, 렌즈 후면이 다른 곡률을 갖고 있는 원시 보정렌즈의 광학적 수차 특성과 성능평가를 비교해 볼 수 있다. 이를 위하여, 정점 구를 원시 보정렌즈 후면에 적용하여 굴절성 원시 모델 안과 함께 최적화 과정을 통하여 설계하고, 그 광학적 수차 특성을 정시 모델 안이 갖고 있는 광학적 수차 특성과 비교해 보았다. 그리고 그에 따른 스톱의 위치에 대해서도 살펴보았다.
대상 및 방법
비정시 보정용 렌즈에 사용되는 렌즈 매수는 한매의 렌즈를 사용하여 보정한다. 한매의 렌즈를 가지고 수차를 보정하는 데에는 자유도가 그리 많지 않다. 따라서 이러한 렌즈의 수차를 보정하는 데 가장 큰 영향을 끼치는 것은 렌즈 형상으로 그 변화에 따라 수차량이 변화됨을 알 수 있다. 단일렌즈에서 구면수차는 렌즈의 형상계수가 +0.7인 경우인 양 복록 렌즈의 형태에서 최소 구면수차가 나타남을 볼 수가 있다. 그러나 비점수차와 같은 경우는 형상계수가 +2.0 근처인 메니스커스 형상에서 수차를 많이 줄일 수 있다.[4] 단일렌즈인 비정시 보정용 렌즈의 수차를 줄일 수 있는 변수로 사용할 수 있는 것에는 렌즈 형상 외에 굴절률, 렌즈 두께, 그리고 스톱의 위치를 생각할 수 있다.
본 논문의 원시 보정용 렌즈의 초기 설계에서는 정점 구의 곡률 반경을 눈의 회전 중심점에 가상의 스톱이 있다고 가정하고, 그 값을 27 mm로 하고 보정렌즈의 후면의 곡률 반경을 정하였다. 그리고 FOV는 30°로 하고 설계하였다. 또한 렌즈 전면의 곡률 반경은 렌즈의 근사적 전체 굴절력 값을 통하여 구하였다. 보정렌즈 설계 시 사용된 초점거리는 유효초점거리(단위:mm)를 사용하였다. 원시 보정용 렌즈는 +1.00 D원시안, +4.00 D원시안, +8.00 D원시안, 그리고 +11.00 D원시안 각각에 대해 초기 설계를 하였다. 이러한 초기설계를 위해 사용된 식은 다음과 같다.[5]
| (1) |
여기에서
여기에서, FA는 보정렌즈의 전체굴절력이고, F1은 전면굴절력, 그리고 F2는 후면굴절력이다. 그리고 r1은 전면의 곡률반경, r1는 후면의 곡률반경을 말하며 n은 보정렌즈의 굴절률이다. 이렇게 하여 얻어진 렌즈의 전체굴절력에 두께를 부여하고 유효굴절력을 구하였다. 중심두께와 유효굴절력을 구하기 위해 사용된 식은 다음과 같다.[5]
| (2) |
| (3) |
여기에서, tC는 중심두께, tP는 가장자리 두께 그리고 h는 렌즈 직경의 반이다. 그리고 FE는 유효 굴절력이다. 위 식을 사용하여 얻은 전면의 곡률반경, 두께 그리고 유효굴절력과 사용된 렌즈의 굴절력 값을 초기 설계 값으로 정하고 Table 1에 나타내었다.
결과 및 고찰
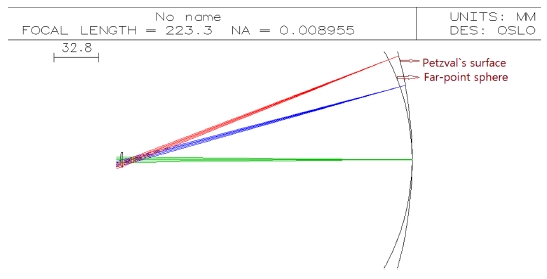
Table 1에 나타난 초기 설계 값을 갖고 우선 원시 보정용 렌즈에만 유효초점거리에 가중치를 두고, 비축 물점에서 나오는 수차를 줄이기 위해 전면의 곡률과 스톱의 위치를 변수로 정하고 설계하여 최적의 스톱의 위치를 정하였다. 그리고 여기에서 얻은 설계 값을 굴절성 원시 모델안과 함께 광선수차를 이용한 최적화 기법을 통하여 최종 설계를 하였다. 이렇게 하여 얻어진 결과를 Table 2에 나타내었다. 또한 4 종류의 원시안 중 +4.00 D원시안과 이에 해당하는 굴절성 원시 모델안과 함께 최종 설계한 결과를 Table 3에 나타내었다. 최적화 과정을 위해 사용된 프로그램은 Lambda Research사의 OSLO를 사용하였다. Fig. 1은 최종 설계된 +4.00 D의 원시 보정용 렌즈의 굴절력 오차(power error)를 보여주고 있다. 여기서, 굴절력 오차 값은 –4.98 D이다. Fig. 1에서 나타난 Petzval`s 면(Petzval`s surface)이 원점 구(far-point sphere)보다 곡률반경이 더 크게 나타난 것은 최적화 과정을 통한 원시 보정렌즈 설계 시 상의 곡률이 미 보정(undercorrets)되었다는 것을 보여주고 있다.

Final design of the corrective lens of a power of +4.00 D with the refractive ametropic eye model (unit: mm)
최종 설계된 설계 값으로부터 광학적 수차 특성 비교를 위해 사용된 정시 모델 안은 한국인 정시 75안을 대상으로 측정되어진 자료로 만들어진 모델 안을 사용하였다.[6] 여기서 사용된 정시 모델안의 전체굴절력은 +63.87 D이고, 유효초점거리는 15.656867 mm이다. 굴절성 원시 모델 안은 후천적 요인인 수정체 만곡도의 변화로 발생되는 굴절성 원시 모델 안을 적용하였다. 여기서, +1.00 D에 해당하는 전체굴절력을 +62.87 D, 그리고 이에 해당하는 유효초점거리는 15.905903 mm이다. +4.00 D의 전체굴절력은 +59.87 D, 유효초점거리는 16.702929 mm이고, +8.00 D의 전체굴절력은 +55.87 D, 유효초점거리는 17.898777 mm이다. 또한 +11.00 D의 전체굴절력은 +52.87 D, 유효초점거리는 18.914411 mm이다.
1차로 보정된 원시 보정용 렌즈를 이와 같은 굴절성 원시 모델 안에 각각 적용하여 최종설계를 하였다. 최적화 과정을 통한 최종 설계 시에도 유효초점거리에 가중치를 두고 렌즈 두께와 스톱 위치를 변수로 정하고 설계하였다. 이 때 FOV는 안구의 최대 회선각도인 20°를 고려하여 최대 30o까지 5o 간격으로 그 광학적 수차 특성과 MTF 특성 등을 살펴보았다. Fig. 2는 비점수차(A), 상면만곡수차(B), 그리고 왜곡수차(C)를 FOV 5o 간격으로 30o까지 Seidel 3차 수차 값으로 나타내었다. 여기서, Seidel 3차 수차 값의 단위는 없다. 그리고 FOV 30o까지 최종 설계에서 나타난 비점수차, 상면만곡수차의 광선수차도의 모양은 정시 모델 안에서 나타난 광선수차도의 모양과 비슷하게 나타났다. Fig. 2A 비점수차를 보면 중심시야 FOV 5o에서 정시 모델 안의 수차 값은 –0.001276인데, 4종류의 원시 보정렌즈의 수차 값과 비교해 보았을 때 10-4 이하 값에서 차이가 나타났으며, 이 값 이하에서 원시 보정렌즈의 수차 값이 적게 나왔다. 그리고 안구 회선 각도를 고려한 20o에서는 정시 모델 안 수차 값이 –0.022082인데, 이 들 비점수차 값은 10-2 이하 값에서 차이가 나타났으며, 이 수차 값에서 원시 보정렌즈의 수차 값이 적게 나타났음을 Fig. 2A를 통해 볼 수 있다. 또한 주변시야에 해당하는 FOV 30o에서 정시 모델 안의 수차 값은 –0.055563이다. 이 경우도 Fig. 2A에서 볼 수 있듯이 정시 모델 안의 수차 값과 비교했을 때 10-2 이하 값에서 차이가 나타났으며, Fig. 2A를 통해 원시 보정렌즈의 값들이 적게 나왔음을 볼 수 있다. 또한 Fig. 2A를 통해 볼 수 있듯이 주변시야로 갈수록 수차 보정이 잘 이루어졌음을 볼 수 있고, 보정렌즈 굴절력이 클수록 수차 값이 적게 나왔음을 볼 수 있다. Fig. 2B는 정시 모델 안이 갖고 있는 상면 만곡수차와 최적화 과정을 통해 얻은 4종류의 원시 보정렌즈의 Seidel 3차 수차 값들을 나타내고 있다. Fig. 1을 통해 볼 수 있듯이 최적화 설계 시 상의 곡률이 미 보정된 굴절력 오차(power error)를 볼 수 있고, 수차 값은 정시 모델 안이 갖고 있는 수차와 비슷하게 나왔지만 주변시야로 가면서 조금 좋게 나오지 않았음을 볼 수 있다. 그리고 비점수차와 상면만곡수차의 Seidel 3차 수차 값을 비교해 보면 상면 만곡 수차 값이 더 크게 나타났음을 두 그림을 통해 또한 볼 수 있다. 그리고 Fig. 2C 왜곡수차를 나타내고 있다. 이 그림에서도 주변시야로 갈수록 굴절성 원시 모델 안과 함께 설계한 원시 보정렌즈의 Seidel 3차 수차 값들이 적게 나왔음을 볼 수 있다. 여기에서도 보정렌즈의 굴절력이 증가할수록 수차 값이 적게 나왔다. 또한 FOV 20o에서 왜곡수차를 백분율로 나타내면 +1.00 D의 경우는 –2.5% 정도, +4.00 D은 –1.9% 정도, +8.00D은 –1.3% 정도, 그리고 +11.00 D은 –0.8% 정도로, 굴절력이 커질수록 왜곡수차가 적게 나왔음을 볼 수 있고, 이를 직사각형 격자모양으로 나타냈었을 때 술통형(barrel type) 형태를 보이고 있다. Table 2에 나타낸 최적화 과정을 통한 최종설계에서 원시 보정렌즈의 전, 후면 곡률반경 값들을 보여주고 있다. 이 값들은 원시 보정렌즈의 근사적 전체굴절력 값 +1.00 D, +4.00 D, +8.00 D, 그리고 +11.00 D 값들로, 그 값들이 변화지 않고 유지시켰음을 볼 수 있다. 그러나 최종 설계에서 나타난 두께 값들의 변화로 이 들의 유효초점거리는 변화됨을 알 수 있다.
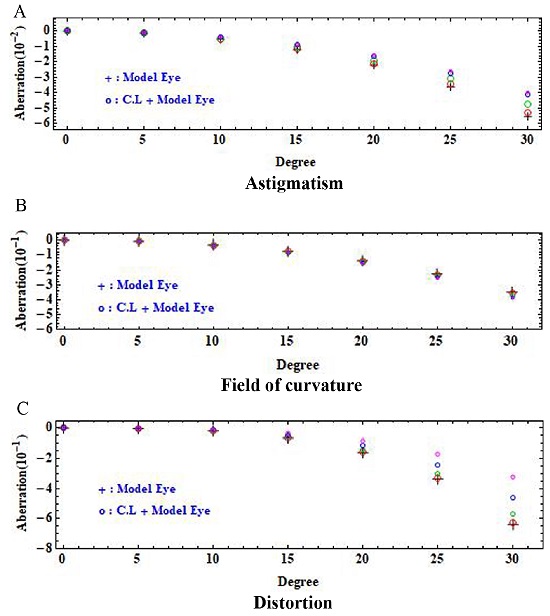
Seidel third-order aberrations of the corrective lenses of powers of +1.00, +4.00, +8.00, and +11.00 D for astigmatism (A), field of curvature (B), and distortion (C).
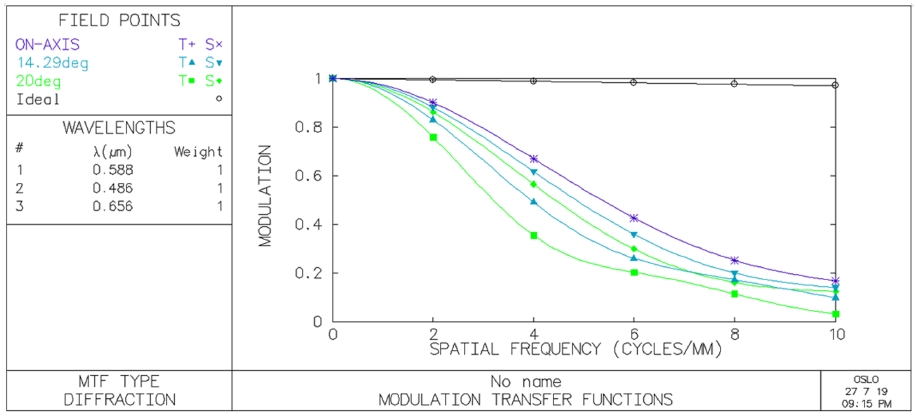
Fig. 3은 FOV 20°에서 정시 모델 안의 MTF 특성을 보여주고 있다. 시력이 1.0인 사람의 눈의 한계 분해능은 대략 1arc min으로 명시거리 250 mm에서 대략 공간주파수 6.88 lp/mm 정도에 해당하는 흑, 백막대로 구성된 표적을 분해할 수 있다.[7] 이 값에서 정시 모델 안의 경우 자오면과 구결면 모두에서 20% 정도의 MTF 값을 보여주고 있다. 굴절성 원시 모델안과 함께 설계한 원시 보정렌즈의 MTF 값들을 보면, 자오면과 구결면 모두에서 +1.00 D의 경우 30%, +4.00 D의 경우 50%, +8.00 D의 경우 62%, 그리고 +11.00 D의 경우는 33% 정도의 값이 나왔다. 그리고 최종 설계 값을 나타낸 Table 2에서 볼 수 있듯이 최적화 과정을 통해 얻은 스톱의 위치는 +1.00 D에서 16.22235 mm, +4.00 D에서 12.362663 mm, +8.00 D에서 10.589072 mm, 그리고 +11.00 D에서 9.820404 mm의 값들이 나와 보정렌즈의 굴절력이 증가할수록 스톱의 위치가 짧아지는 모습을 보이고 있다.
결 론
원시 보정렌즈 후면에 유효굴절력이 작용하지 않는 곡률반경을 적용하여 렌즈 전면의 곡률반경만을 가지고 원시 모델 안과 함께 최적화 과정을 통하여 설계하고, 그리고 정시 모델 안과 그 광학적 수차 특성과 성능평가를 비교해 보았다. 또한 원시 보정렌즈의 전체굴절력 값이 변하지 않도록 최종 설계하였다. 그리고 이들의 광학적 수차 특성을 비교해 본 결과, 상면만곡수차는 정시 모델 안 이 갖고 있는 수차 특성과 비슷하게 나타났음을 볼 수 있었고, 비점수차는 상면만곡수차 보다 특성이 좀 더 좋게 나타났음을 볼 수 있었다. 특히 비점수차는 중심시야에서는 정시 모델 안과 비슷한 수차 특성을 보였지만 주변시야로 가면서 정시 모델 안보다 좋은 수차 특성을 보였다. 또한 원시 보정렌즈 굴절력이 클수록 수차 보정이 좋게 나온 특성을 보였다. 왜곡수차 또한 주변시야로 가면서 수차 특성이 좋게 나타났음을 볼 수 있었고, 이 또한 보정렌즈의 굴절력이 클수록 수차 특성이 잘 나타났음을 볼 수 있었다. 정시 모델안과 비교한 성능평가는 정시안의 경우 한계 분해능을 측정하는 공간 주파수 7l p/mm 정도에서 자오면과 구결면 모두에서 20% 정도의 값으로, +1.00 D원시안에서 30%정도, +4.00 D원시안에서 50%, +8.00 D원시안에서 62%, 그리고 +11.00 D원시안에서 33% 정도의 값이 나왔다. 그리고 만곡도가 매우 심한 경우에 해당하는 정점 구의 렌즈 형상에서 보여준 광학적 수차특성과 성능 평가를 토대로, 주변시야 수차보정을 하는데 있어서 렌즈의 만곡도가 영향을 미친다는 것을 알 수 있었고, 또한 비교, 평가 할 수 있는 비교 자료로도 활용할 수 있을 것으로 생각된다. 그리고 최적화 과정 중 스톱 위치의 변화는 원시 보정렌즈의 굴절력이 커질수록 그 거리가 짧아지는 특징을 보였다.
REFERENCES
- Fannin TE, Grosvenor T. Clinical optics, 2nd Ed. London: Butterworth-Heinemann, 1996;133-153.
-
Brooks C, Borish I. System for ophthalmic dispensing, 3rd Ed. Philadelphia: Butterworth-Heinemann, 2007;22-25.
[https://doi.org/10.1016/B978-0-7506-7480-5.50007-1]

- Morris MA, Perrott CM, Spratt RS. Wide Field Spherical Lenses and Single Design Spectacle Frames Therefor. U.S. Patent 6142624, 2000.
- Jenkins FA, White HE. Fundamentals of optics, 4th Ed. New York: McGRAW-Hill, 1976;153-157.
- Shannon RR, Wyant JC. Applied optics and optical engineering, vol. 3. New York: Academic press, 1965;237-238.
-
Kim SG, Park SC. Optimum design of the finite schematic eye using spherical aberration. Korean J Opt. 2002; 13(3):266-271.
[https://doi.org/10.3807/KJOP.2002.13.3.266]

-
Park SC, An HK. Lens system design for head mounted display using schematic eyes. Korean J Opt. 2003;14(3):236-243.
[https://doi.org/10.3807/KJOP.2003.14.3.236]