[ Article ]

Journal of Korean Ophthalmic Optics Society - Vol. 22, No. 3, pp.253-260

ISSN: 1226-5012 (Print)

Print publication date 30 Sep 2017

Received 31 Jul 2017 Revised 22 Aug 2017 Accepted 29 Aug 2017

DOI: https://doi.org/10.14479/jkoos.2017.22.3.253

굴절력 매트릭스에 근거한 Javal법칙의 신뢰도

유동식

; 조현국

; 김상엽 ; 김형수 ; 문병연^*

강원대학교 안경광학과, 삼척 25949

Reliability of Javal’s Rule Based on Dioptric Power Matrix

Dong-Sik Yu

; Hyun Gug Cho

; Sang-Yeob Kim, ; Hyeong-Su Kim, ; Byeong-Yeon Moon^*

Dept. of Optometry, Kangwon National University, Samcheok 25949, Korea

Correspondence to: ^*Byeong-Yeon Moon, TEL: +82-33-540-3412, E-mail: bymoon@kangwon.ac.kr

초록

목적

각막난시로부터 굴절난시를 예측하는 여러 버전의 Javal법칙의 신뢰도를 굴절력 매트릭스를 근거하여 평가하고자 하였다.

방법

총 84명(168안, 평균 24.67±1.59세)의 대상자가 참여하였다. 각막난시(corneal astigmatism, Ac)는 자동각막굴절력계로 측정하였고, 원상태의 Javal법칙(original Javal’s rule, OJR), 단순화된 Javal법칙(simplified Javal’s rule, SJR), Yoo 등의 회귀식(Yoo’s regression equation, YRE)과 굴절력 벡터의 Javal법칙(vector-based Javal’s rule, VJR) 등의 4가지 버전을 이용하여 Ac로부터 굴절난시(refractive astigmatism, At)를 굴절력 매트릭스에 의해 예측하였다. 자각적으로 결정되는 굴절난시(SAt)는 최대교정시력으로 하였다.

결과

각막난시 축과 예측된 굴절난시의 축의 상관관계는 높았고(r = 0.891~0.971, p<0.001), 예측한 굴절난시 축과 자각적으로 결정된 굴절난시 축의 상관성은 모두 낮았다(r = 0.182~0.223, p = 0.004~0.018). 상대적 신뢰도를 나타내는 대응비교에서 굴절력 벡터의 Javal 법칙으로 예측된 굴절난시와 자각적으로 결정된 굴절난시가 각각 0.80±0.58 D과 0.82±0.65 D로 유의한 차이를 보이지 않았다(p = 0.662). 절대적 신뢰도를 나타내는 Bland-Altman 분석에서 굴절력 벡터의 Javal법칙에서 예측된 굴절난시와 자각적으로 결정된 굴절난시의 평균차이는 –0.02±0.51 D로 작았다. 구원주 굴절력의 비교에서 예측된 굴절난시와 자각적으로 결정된 굴절난시의 차이는 굴절력 벡터의 Javal법칙, 단순화된 Javal법칙, Yoo 등의 회귀식, 원상태의 Javal법칙 순으로 작았다. 구간별 비교에서 원상태의 Javal법칙이 모든 구간(≤2.00 D)에서 낮은 빈도를 보였고, 0.75 D 이하의 낮은 구간에서 굴절력 벡터의 Javal법칙이 높은 빈도를 보였다. 예측된 굴절난시가 자각적으로 결정된 굴절난시보다 큰 경우와 작은 경우의 사이에서 각막난시 항의 최적 상수는 1.00과 0.79 범위로 예상할 수 있었다.

결론

각막난시부터 굴절난시의 예측은 굴절력 벡터의 Javal법칙이 더 신뢰가 높으며, 굴절력 벡터가 아닌 산술적으로 간단한 임상적 예측에서 Javal법칙에 적용되는 각막난시의 상수는 1.0~0.79 범위가 될 것으로 본다.

Abstract

Purpose

To evaluate the reliability of several versions of Javal’s rule predicting refractive astigmatism from corneal astigmatism on the basis of dioptric power matrix.

Methods

A total of 84 subjects (168 eyes, mean age 24.67±1.59 years) participated in this study. Corneal astigmatism (Ac) was measured by auto kerato-refractometer. Refractive astigmatism (At) was predicted by dioptric power matrix using four versions of original Javal’s rule (OJR), simplified Javal’s rule (SJR), Yoo’s regression equation (YRE), and vector-based Javal’s rule (VJR) from Ac. The subjectively determined refractive astigmatism (SAt) was taken best corrected visual acuity.

Results

The relations between axes of Ac and At were represented high values (r = 0.891 to 0.971, p<0.001), the relations between axes of At and SAt were represented low values (r = 0.182 to 0.223, p = 0.004-0.018) for all four versions. The mean magnitudes of At and SAt for the VJR were 0.80±0.58 D and 0.82±0.65 D respectively. The difference between two values was not significant in paired t-test as relative reliability (p = 0.662). In Bland-Altman analysis as absolute reliability, the mean difference of At and SAt for the VJR had a small bias of –0.02±0.51 D. In comparison of previous cylindrical power, the difference between At and SAt was decreased in order of OJR, YRE, SJR, and VJR. In those of differences, OJR showed the lowest distribution within all intervals (≤ 2.00 D), VJR showed the highest distribution at the less than 0.75 D. The anticipated constant optimization were range from 0.79 to 1.00 for corneal astigmatism as the differences between At and SAt were the boundaries between more and less.

Conclusions

Vector-based Javal’s rule is more reliable in predicting refractive astigmatism from corneal astigmatism, and the constant of 0.79 to 1.00 for corneal astigmatism in Javal’s rule except this rule may be applied in clinical prediction with simplicity by arithmetic operation.

Keywords:

Javal’s rule, Dioptric power matrix, Astigmatism, Vector, Refractive astigmatism, Corneal astigmatism

키워드:

Javal법칙, 굴절력 매트릭스, 난시, 벡터, 굴절난시, 각막난시

서 론

Javal법칙^[1,2]은 굴절검사를 실행하기 전에 측정된 각막난시(corneal astigmatism, Ac)로부터 전체난시, 즉 굴절난시(total astigmatism 또는 refractive astigmatism, At)를 예측하거나 안구매체가 불투명하여 검영법을 수행할 수 없을 때 굴절난시를 예측할 수 있는 방법으로 임상에 적용되고 있다.^[3-5]

원상태의 Javal법칙(original Javal’s rule, OJR)^[2,6]은 각막난시를 1.25배로 하고, 여기에 0.50 D의 직난시를 합산하여 굴절난시를 예측할 수 있는 방법이다. 여러 연구자들은 이 방법의 타당성을 평가하였고 여러 가지 수정된 버전의 Javal법칙을 제시하였다.^[7-9] Grosvenor 등^[6]은 각막난시에 0.50 D의 직난시를 합산하여 굴절난시를 예측하는 단순화된 Javal법칙(simplified Javal’s rule, SJR)을 제시하였고, 이외에도 Sutcliff, O’Shea, Neumueller 등도 제안하였다.^[10] Yoo 등^[11]은 한국인 20대를 대상으로 각막난시에 따른 굴절난시를 각막난시의 0.79배와 0.49 D의 직난시의 합으로 나타내는 회귀식(Yoo’s regression equation, YRE)을 제시하였다. 이러한 여러 버전의 Javal법칙은 각막이 직난시 또는 도난시이며, 합산되는 잔여난시(수정체난시)와 축이 일치하거나 직교함으로 굴절난시를 쉽게 산술적으로 계산할 수 있으나^[3] 각막이 사축(oblique axis)인 경우 정확한 계산을 할 수 없고, 단지 직난시와 도난시에 가까운 축에 한하여 근사적으로 계산하였다.^[12]

지금까지 제시된 Javal법칙에 대한 평가는 각막난시와 굴절난시의 상관관계와 그것의 타당성을 중심으로 이루어졌고, 적용 가능한 각막난시는 대부분 직난시나 도난시로 한정하였다. 한편, Tong 등^[13]은 이를 사난시까지 확장하였으며, 산술적 계산보다 굴절력 벡터(power vector)^[14,15]를 근거한 Javal법칙(vector-based Javal’s rule, VJR)을 제안하였다. 즉, 난시의 굴절력을 90도와 180도 경선의 직교성분(J₀)과 45도와 135도 경선의 사난시 성분(J₄₅)으로 나누어 예측식을 제시하였다. 이러한 굴절력 벡터에 의한 평가는 통계 처리 측면에서 이점이 있으나^[16] 난시의 굴절력과 축으로 표현하는 전통적 형식과 다르므로 임상 적용에는 용이하지 않다.

굴절력의 또 다른 표기 방법은 굴절력 매트릭스(dioptric power matrix)^[12,17,18]로 가능하며 이를 Javal법칙에 적용한다면 난시의 종류에 관계없이 Javal법칙을 평가할 수 있을 것이다. 아직까지 굴절력 매트릭스를 기반으로 Javal법칙을 평가한 연구는 이루어지지 않고 있다. 따라서 본 연구에서는 굴절력 매트릭스 기반으로 제시된 여러 형태의 Javal법칙의 신뢰도를 평가하고자 하였다.

대상 및 방법

1. 대상

본 연구의 취지에 동의한 20대 84명(168안; 연령 24.67±1.59세; 남자 56, 여자 28)을 대상으로 하였다. 대상자 모두 전신질환이나 안질환이 없으며, 굴절이상이나 안기능이상으로 인한 눈 수술 경험은 없었다. 굴절검사를 실시하여 최대교정시력이 1.0에서 1.2의 근시안을 대상으로 하였다.

2. 연구 방법

굴절력과 각막곡률은 자동굴절력계(KR-8800, Topcon, Japan)로 3회 측정하였고, 자각적 굴절검사는 수동 포롭터(Phoropter 11625B, Reichert, USA)를 이용하여 실시하였다. 각막난시는 steep한 경선에서 flat한 경선의 차이로 결정하였고, 굴절난시는 최대교정시력에서의 교정 굴절력으로 정점간거리 0(zero) mm를 기준으로 결정하였다.

본 연구에서 여러 버전의 Javal법칙의 신뢰도 평가에 적용된 선택 기준과 제시된 식은 다음과 같다. 첫 번째는 1890년에 제시된 원상태의 Javal법칙으로 식 (1)이며, 두번째는 수정된 방법으로 단순화된 Javal법칙으로 식 (2), 그 다음은 한국인 20대를 대상으로 Yoo 등의 회귀식으로 제시한 식 (3)이며, 마지막으로 아동(7~13세)을 대상으로 원상태의 Javal법칙과 단순화된 Javal법칙보다 더 정확하게 예측 가능하다고 한 굴절력 벡터의 Javal법칙으로 식 (4)와 식 (5)이다.

O r i g i n a l J a v a l' s r u l e :

(1)

A t = 1.25 × A c + C - 0.50 × 90

S i m p l i f i e d J a v a l' s r u l e :

(2)

A t = A c + C - 0.50 × 90

Y o o' s r e g r e s s i o n e q u a t i o n :

(3)

A c = 0.79 A c + C - 0.49 × 90

V e c t o r - b a s e d J a v a l' s r u l e :

(4)

A t J 0 = 0.931 × A c J 0 - 0.276

A t J 45 = 0.638 × A c J 45 - 0.010

(5)

여기서 At = refractive astigmatism, Ac = corneal astigmatism, C = cylindrical power, AtJ₀ = J₀ vector refractive astigmatism, AcJ₄₅ = J₄₅ vector corneal astigmatism이다.

굴절력 벡터의 Javal법칙을 제외한 3가지 식들은 굴절력 매트릭스 형식^[18]으로 계산하여 S-C표기로 전환한 다음 평가하였다. 굴절력 벡터의 Javal법칙은 각막난시를 식 (6)과 식 (7)로 분리하여 표기하였다.

J 0 = - C / 2 cos ⁡ 2 × a x i s

(6)

J 45 = - C / 2 sin ⁡ 2 × a x i s

(7)

J₀와 J₄₅의 각막난시에 따른 굴절난시를 식 (4)와 식 (5)으로 계산한 다음, 식 (8)과 식 (9)에 대입하여 결정하였다.

C = - 2 × A t J 0 2 + A t J 45 2 1 / 2

(8)

A x i s = 1 / 2 t a n - 1 A t J 45 / A t J 0

(9)

이렇게 결정된 굴절난시는 굴절력 매트릭스 형식으로 계산하고 S-C표기로 전환한 다음 평가하였다.

3. 분석

각막난시로부터 예측된 굴절난시와 자각적으로 결정된 굴절난시는 S-C표기 기준으로 평가하였고, 통계분석에서 난시는 절대량으로 하였다. MedCalc^®(version 10.3.1.0, MedCalc Software bvba, Belgium)을 이용하여 기술통계, paired t-test, 상관분석 및 Bland-Altman분석을 실시하였다. 모든 분석에서 신뢰구간은 95%로 하였고, 유의 확률(p)<0.05일 때 통계적으로 유의한 것으로 판단하였다.

결과 및 고찰

1. 대상자의 난시의 특성

84명의 근시안(168안)을 대상으로 각막난시로부터 굴절난시를 예측·평가하는 데 필요한 굴절력 요소와 난시의 특성은 Table 1과 같다. 굴절난시는 평균 −0.91±0.72 D였고 각막난시는 −1.38±0.72 D였다. 이는 Yoo 등^[11]의 연구에서 대상자의 평균 굴절난시 −0.53±0.77 D보다 0.38 D 높으며, 각막난시 −1.30±0.71 D와 유사하다. 굴절난시의 분포는 직난시 74.4%, 도난시 5.9%, 사난시 4.2%, 난시가 없는 경우가 15.5%였다. 이는 Yoo 등이 발표한 굴절난시에서 직난시 78.7%, 도난시 21.3%로 분포되어 있는 것과 달리 난시가 없는 대상자의 빈도가 높았다. 각막난시는 직난시 95.8%, 도난시와 사난시가 각각 1.8%, 난시가 없는 경우가 0.6%로 굴절난시에 비해 직난시가 21.4% 많았고, 난시가 없는 경우가 14.9%, 도난시와 사난시는 각각 4.1%, 2.4% 적었다. 이는 Yoo 등이 발표한 각막난시에서 직난시가 92.5%, 도난시가 1%, 사난시가 6.5%로 굴절난시에 비해 직난시는 13.8%, 사난시는 6.5%가 많았으며, 도난시는 20.3% 적은 것과 비교할 때^[11] 직난시의 비중은 3.3% 높았고, 사난시의 비중이 4.7% 낮았다.

Table 1.

Distribution of refractive astigmatism and corneal astigmatism of subjects

2. 굴절력 매트릭스에 의한 굴절난시 예측

각막난시와 도난시성 수정체난시(잔여난시)로 구성되는 Javal법칙은 그 구성 성분의 크기와 상수에 따라 굴절난시가 결정된다.^[6] 따라서 산술식 형태의 Javal법칙은 직난시와 도난시로 구분되는 이분적 예측이며 사난시를 예측할 수 없다. 그러나 굴절력 매트릭스에 의한 예측은 사난시 예측도 가능한 방법이다. 각막난시로부터 굴절난시를 예측하는 여러 버전 중에서 원상태의 Javal법칙, 단순화된 Javal법칙, Yoo 등의 회귀식 및 굴절력 벡터의 Javal법칙을 중심으로 굴절력 매트릭스에 의해 예측된 굴절난시의 분포는 Table 2와 같다.

Table 2.

Distribution of the refractive astigmatism predicted by dioptric power matrix

직난시로 예측되는 비율은 굴절력 벡터의 Javal법칙을 제외하고 원상태의 Javal법칙, 단순화된 Javal법칙, Yoo 등의 회귀식 순으로 높았다. 이는 각막난시에 적용되는 상수크기의 순서와 동일한 경향을 보였다. 도난시 예측 비율은 Yoo 등의 회귀식에서 13.1%로 높았고 굴절력 벡터의 Javal법칙에서 2.4%로 낮았으며, 사난시로 예측 비율은 단순화된 Javal법칙과 Yoo 등의 회귀식에서 각각 13.1%로 높았다. 자각적으로 결정된 굴절난시와 반대로 직난시가 도난시로 예측되는 비율 또는 도난시가 직난시로 예측되는 비율은 1.8%~3.6%였으며, 단순화된 Javal법칙에서 1.8%로 가장 낮았다. 이러한 예측 현상은 각막난시가 도난시일 때 일어났다. 난시가 없는 것으로 예측되는 비율은 단순화된 Javal법칙에서 1.2%, 나머지 3가지 방법 모두 0%로 거의 없는 것으로 나타났다. Yoo 등의 회귀식에서는 73.8%의 직난시가 예측되었고, 원상태의 Javal법칙과 단순화된 Javal법칙은 각각 6.5%와 5.4%로 도난시가 예측되었으며, 이 결과는 자각적으로 결정된 굴절난시에서 직난시 74.4%, 도난시 5.9%와 유사하다. Javal법칙에서 산술적으로 예측되는 굴절난시의 종류는 식 (1)~식 (3)와 같이 각막난시 항과 수정체난시 항의 비율에 따라 결정된다.^[6] 즉, 각막난시가 직난시인 경우 각막난시 항이 각 식 (1), 식 (2), 식 (3)에서 각각 0.40 D, 0.50 D, 0.62 D 이상이면 굴절난시는 직난시이고, 그 이하면 도난시로 예측할 수 있다. 또한 각막이 도난시인 경우 굴절난시는 도난시로 예측할 수 있고, 사난시의 경우 산술적 예측이 되지 않는다. 그러나 굴절력 벡터나 굴절력 매트릭스에 의해 모든 난시로 예측이 가능하다. 각막난시와 예측된 굴절난시의 축의 상관관계 분석에서 각막난시 항의 비중이 큰 Javal법칙일수록 0.891~0.971로 높은 상관성을 보였다(p<0.001). 그러나 굴절력 벡터의 Javal법칙에서 0.632로 낮은 상관성을 보였다(p<0.001). 굴절난시에서 예측한 축과 자각적으로 결정한 축의 상관관계는 Yoo 등의 회귀식에서 0.223(p = 0.004), 단순화된 Javal법칙에서 0.216(p = 0.005), 굴절력 벡터의 Javal법칙에서 0.211(p = 0.006), 원상태의 Javal법칙에서 0.182(p = 0.018) 순으로 나타났고 상관관계가 낮았다. 이러한 낮은 상관관계는 축의 다양성 차이가 한 요인일 것이다. 즉 자각적으로 결정된 축은 30개로 평가되었고 굴절력 매트릭스에 의한 예측된 축은 100개 이상으로 평가되어 다양성에서 차이를 보였다.

3. 예측된 굴절난시와 자각적으로 결정된 굴절난시의 크기 비교

굴절력 매트릭스에 의해 예측된 굴절난시와 자각적으로 결정된 굴절난시의 신뢰도 분석은 크기의 평균치 비교, 상관관계 및 Bland-Altman 분석 등 상대적 또는 절대적 신뢰도를 평가하였고,^[19] 그 결과는 Table 3과 같다.

Table 3.

Comparisons between predicted and subjectively determined the magnitude of refractive astigmatism

계통 오차(systematic error)에 의해 신뢰도를 나타내는 대응표본 평균치 비교에서 굴절력 벡터의 Javal법칙으로 예측된 굴절난시의 크기는 0.80±0.58 D로 자각적으로 결정된 굴절난시의 크기 0.82±0.65 D와 유의한 차이를 보이지 않았고(p=0.662), 원상태의 Javal법칙, 단순화된 Javal법칙과 Yoo 등의 회귀식에서 각각 1.30±0.84 D(p<0.001), 0.97±0.66 D(p<0.001), 0.71±0.49 D(p=0.004)로 유의한 차이를 보였다. 일관성(consistency)에 의해 상대적 신뢰도를 나타내는 Pearson 상관관계는 원상태의 Javal법칙에서 0.669(p<0.001)로 상대적으로 가장 높은 상관관계를 보였고, Yoo 등의 회귀식에서 0.650(p<0.001)로 상대적으로 가장 낮았다. 일관성과 일치도에 의해 상대적 신뢰도를 나타나는 급내상관계수는 단순화된 Javal법칙에서 0.662로 가장 높았고 Yoo 등의 회귀식에서 0.628로 가장 낮았다. 계통 오차(systematic error)와 일치도에 의해 절대적 신뢰도를 나타내는 Bland-Altman분석^[20]에서 평균차이는 굴절력 벡터의 Javal법칙에서 –0.02±0.51 D로 가장 적었고 원상태의 Javal법칙에서 0.49±0.63 D로 가장 컸다. 또한 95%의 일치도 범위는 Yoo 등의 회귀식에서 –1.09~0.86 D로 가장 좁았고 원상태의 Javal법칙에서 –0.75~1.72 D로 가장 넓었다. 위와 같이 다양한 기준의 신뢰도 분석에서 상대적 신뢰도 기준으로 볼 때 상관계수에서는 원상태의 Javal법칙, 급내상관계수에서는 단순화된 Javal법칙이 높았고 Yoo 등의 회귀식이 가장 낮게 평가되었으나 그 차이는 미미한 것으로 본다. 상대적 신뢰도와 절대적 신뢰도 측면에서는 굴절력 벡터의 Javal법칙에서 높게 평가되었다.

4. 굴절난시의 구원주 굴절력 비교

굴절력 매트릭스에 의해 예측된 굴절난시와 자각적으로 결정된 굴절난시의 차이를 구원주 굴절력(spherocylindrical power)^[21,22]으로 분석하였다. 여기서 구원주 굴절력 분석은 난시의 축과 크기 요소를 고려한 분석을 의미한다.

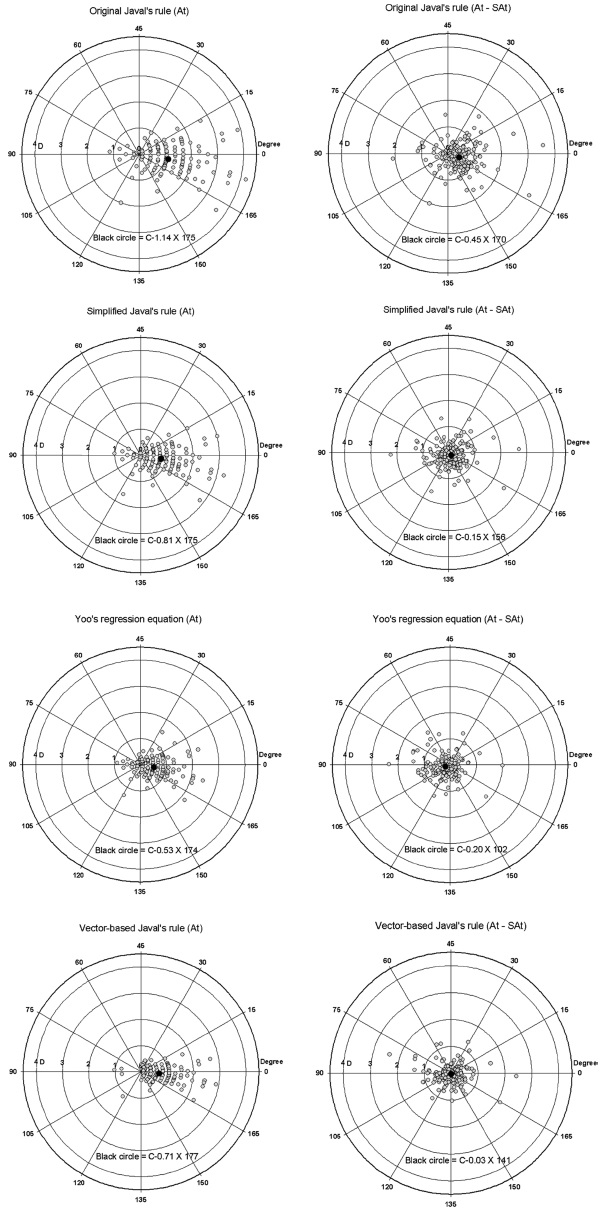
예측된 굴절난시와 자각적으로 결정된 굴절난시의 평균크기와 축(방향)을 비교한 결과는 Table 4와 같다. 예측된 굴절난시는 원상태의 Javal법칙, 단순화된 Javal법칙, 굴절력 벡터의 Javal법칙, Yoo 등의 회귀식 순으로 크기가 컸으며 축은 174°~177° 범위였다. 자각적으로 결정된 굴절난시의 차이는 굴절력 벡터의 Javal법칙에서 0.03 D로 가장 적은 난시 차이를 보였고, 원상태의 Javal법칙에서 0.45 D로 가장 큰 난시 차이를 보였다. 굴절난시 차이(ΔAt) 값에서 (+) 값의 구면 굴절력은 예측된 난시가 자각적으로 결정된 난시보다 작다는 의미이며, Yoo 등의 회귀식과 굴절력 벡터의 Javal법칙에서 나타났다. 이러한 결과는 예측식에서 각막난시 항의 비중이 낮은 경우에 나타났다.

Table 4.

Difference between predicted and subjectively determined refractive astigmatism in spherocylindrical power

굴절난시 차이를 구간별로 평가할 때 0.75 D 이내까지는 굴절력 벡터의 Javal법칙은 80.4% 가장 높았고, 1.00 D이내에서 단순화된 Javal법칙은 90.5%로 가장 높았으며, 1.50 D 이내에서 Yoo 등의 회귀식이 98.2%로 가장 높았다. Elliot 등^[23]의 연구에서 안경난시 기준으로 평가할 때 1.00 D 이내에서 원상태의 Javal법칙과 단순화된 Javal법칙은 각각 92.0%, 94.0% 분포하였고, Yoo 등^[11]의 연구에서 95.4%로 본 연구의 결과보다 높았다. 원상태의 Javal법칙은 모든 구간에서 낮은 빈도를 보였으며 굴절력 벡터의 Javal법칙은 낮은 구간에서 높은 빈도를 보였다.

분석한 결과를 Fig. 1과 같이 난시만을 극도표^[22]로 나타냈을 때 예측된 난시는 원상태의 Javal법칙에서 넓게 분포하는 형태였고 굴절력 벡터의 Javal법칙에서 좁게 분포하였다. 대체적으로 각막난시 항의 비중이 작을수록 굴절난시가 넓게 분포하는 형태였다. 평균치 또한 0(zero)에 근접하였다. 자각적으로 결정된 굴절난시와 차이는 굴절력 벡터의 Javal법칙, 단순화된 Javal법칙, Yoo 등의 회귀식, 원상태의 Javal법칙 순으로 작았다. 굴절력 벡터의 Javal법칙 제외하고 이러한 차이는 예측식과의 경향성, 즉 각막난시 항과의 연관성이 낮다. 그러나 구원주 굴절력(spherocylindrical power) 분석 결과에서 예측된 굴절난시가 자각적으로 결정된 굴절난시보다 큰 경우와 작은 경우의 사이에 최적으로 예측되는 각막난시 항의 상수, 즉 0.79와 1.00 사이에 최적 상수가 있을 것으로 예상할 수 있다. 이러한 예상은 Lam 등^[24]이 제시한 각막상수 0.93과 굴절난시 차이가 가장 적은 굴절력 벡터의 Javal법칙에서 회귀식의 각막난시 상수 0.98을^[13]을 고려할 때 타당성이 있는 것으로 본다.

Fig. 1.

Polar polt for Javal’s rule by diptric power matrix. Left and right rows shown the predicted refractive astigmatism and their difference of the subjectively determined refractive astigmatism (SAt), respectively. Black circles represent mean values.

결 론

각막난시로부터 굴절난시를 예측하는 Javal법칙은 지금까지 대부분이 직난시 또는 도난시에 한정하여 산술적 계산으로 예측하였다. 본 연구에서는 난시를 구분하지 않고 굴절력 매트릭스에 의해 지금까지 제시된 4가지의 Javal법칙, 즉 원상태의 Javal법칙, 단순화된 Javal법칙, Yoo 등의 회귀식과 굴절력 벡터의 Javal법칙의 신뢰도를 평가하였다.

예측된 굴절난시에서 직난시는 Yoo 등의 회귀식에서, 도난시는 원상태의 Javal법칙과 단순화된 Javal법칙에서 자각적으로 결정된 굴절난시의 빈도와 유사하였다. 예측한 굴절난시 축과 각막난시 축의 상관관계는 각막난시 항의 비중이 큰 Javal법칙일수록 높았고(r = 0.891~0.971, p<0.001), 굴절력 벡터의 Javal법칙에서 낮았다(r = 0.632, p<0.001). 예측한 굴절난시의 축과 자각적으로 결정된 굴절난시의 상관성은 4가지의 Javal법칙 모두 낮았다(r = 0.182~0.223, p = 0.004~0.018).

신뢰도 분석에서 상관관계는 원상태의 Javal법칙이 높았고(0.669, p<0.001), 급내상관계수는 단순화된 Javal법칙이 0.662로 높았다. Yoo 등의 회귀식이 가장 낮게 평가되었으나 그 차이는 미미한 것으로 본다. 상대적 신뢰도와 절대적 신뢰도 측면에서는 굴절력 벡터의 Javal법칙에서 높게 평가되었다.

예측된 난시의 분포와 평균은 굴절력 벡터의 Javal법칙을 제외한 다른 예측 방법에서 각막난시의 비중이 낮을수록 좁고 영(0)에 가깝게 분포하였다. 자각적으로 결정된 굴절난시와 차이는 뚜렷한 경향성을 보이지 않았으나 구원주 굴절력으로 분석 결과에서 예측식의 각막난시 상수가 0.79와 1.00 사이가 최적 상수로 예상할 수 있었다. 따라서 굴절력 벡터가 아닌 임상적으로 간단한 산술적 예측시 Javal법칙에 예상되는 최적 상수를 활용할 수 있을 것으로 본다. 굴절난시 차이를 구간별 비교에서 모든 구간에서 원상태의 Javal법칙이 낮은 빈도를 보였고, 0.75 D 이하의 낮은 구간에서 굴절력 벡터의 Javal법칙이 높은 빈도를 보였다.

평가한 Javal법칙들에서 신뢰가 높은 방법은 굴절력 벡터의 Javal법칙이며, 임상적으로 간단한 산술적 예측은 각막난시의 상수가 0.79~1.00 범위가 적절할 것으로 본다.

References

Benjamin, W, Borish's clinical refraction, 2nd Ed, St. Louis, Butterworth-Heinemann, (2006), p655.
Schwartz, SH, Geometric and visual optics: a clinical introduction, 1st Ed, New York, McGraw-Hill, (2002), p219-221.
Grosvenor, T, Primary care optometry, 5th Ed, St. Louis, Butterworth-Heinemann, (2007), p186-188.
Asiedu, K, Kyei, S, Ampiah, EE, Autorefraction, retinoscopy, Javal's rule, and Grosvenor's modified Javal's rule: the best predictor of refractive astigmatism, J Ophthalmol, (2016), 2016, p3584137. [https://doi.org/10.1155/2016/3584137]
Motlagh, MG, Validity of simlified Javal’s Rule in 147 pre-operation cataract eyes, World Academy of Science Engineering and Technology International Science Index, (2015), 1(2), p630.
Grosvenor, T, Quintero, S, Perrigin, DM, Predicting refractive astigmatism: a suggested simplification of Javal’s rule, Am J Optom Physiol Opt, (1988), 65(4), p292-297.
Mote, HG, Fry, GA, The significance of Javal's rule, Am J Optom Arch Am Acad Optom, (1939), 16(10), p362-365. [https://doi.org/10.1097/00006324-193910000-00001]
Kratz, JD, Walton, WG Jr, A modification of Javal's rule for the correction of astigmatism, Am J Optom Arch Am Acad Optom, (1949), 26(7), p295-306. [https://doi.org/10.1097/00006324-194907000-00004]
Grosvenor, T, Ratnakaram, R, Is the relation between keratometric astigmatism and refractive astigmatism linear?, Optom Vis Sci, (1990), 67(8), p606-609. [https://doi.org/10.1097/00006324-199008000-00009]
Neumueller, J, Optical, physiological and perceptual factors influencing the ophthalmometric findings, Am J Optom Arch Am Acad Optom, (1953), 30(6), p281-291.
Yoo, JS, Yu, DS, Han, KA, Kim, SJ, Wi, SH, Estimation of total astigmatism quantity from corneal astigmatism on Koreans in their twenties, J Korean Ophthalmic Opt Soc, (2008), 13(4), p151-154.
Yu, DS, Yoo, JS, Predicting powers of spherical rigid gaspermeable lenses prescription, J Korean Ophthalmic Opt Soc, (2010), 15(3), p219-225.
Tong, L, Carkeet, A, Saw, SM, Tan, DT, Corneal and refractive error astigmatism in Singaporean schoolchildren: a vector-based Javal's rule, Optom Vis Sci, (2001), 78(12), p881-887. [https://doi.org/10.1097/00006324-200112000-00010]
Raasch, T, Clinical refraction in three-dimensional dioptric space revisited, Optom Vis Sci, (1997), 74(6), p376-380. [https://doi.org/10.1097/00006324-199706000-00020]
Miller, JM, Clinical applications of power vectors, Optom Vis Sci, (2009), 86(6), p599-602. [https://doi.org/10.1097/opx.0b013e3181a6a211]
Thibos, LN, Wheeler, W, Horner, D, Power vectors: an application of Fourier analysis to the description and statistical analysis of refractive error, Optom Vis Sci, (1997), 74(6), p367-375. [https://doi.org/10.1097/00006324-199706000-00019]
Harris, WF, Power vectors versus power matrices, and the mathematical nature of dioptric power, Optom Vis Sci, (2007), 84(11), p1060-1063. [https://doi.org/10.1097/opx.0b013e318157acbb]
Colliac, JP, Matrix formula for intraocular lens power calculation, Invest Ophthalmol Vis Sci, (1990), 31(2), p374-381.
Bruton, A, Conway, JH, Holgate, ST, Reliability: what is it and how is it measured?, Physiotherapy, (2000), 86(2), p94-99. [https://doi.org/10.1016/s0031-9406(05)61211-4]
Bland, JM, Altman, DG, Statistical methods for assessing agreement between two methods of clinical measurement, Lancet, (1986), 1(8476), p307-310.
Kreda, S, How to refine toric lens prescriptions: you can simplify the process of measuring crossed cylinders by applying the principles of vector analysis to optics, Optometric Management, (2012), 47(4), p44-46.
Hollady, JT, Dudeja, DR, Koch, DD, Evaluating and reporting astigmatism for individual and aggregate data, J Cataract Refract Surg, (1998), 24(1), p57-65.
Elliott, M, Callender, MG, Elliott, DB, Accuracy of Javal’s rule in the determination of spectacle astigmatism, Optom Vis Sci, (1994), 71(1), p23-26. [https://doi.org/10.1097/00006324-199401000-00005]
Lam, AK, Chan, CC, Lee, MH, Wong, KM, The aging effect on corneal curvature and the validity of Javal's rule in Hong Kong Chinese, Curr Eye Res, (1999), 18(2), p83-90. [https://doi.org/10.1076/ceyr.18.2.83.5384]

Parameter		Mean±SD (range)
†Based-spectacle. ‡Based-spectacle at vertex distance zero. SD: standard deviation, Sph: spherical power, Cyl: cylindrical power, SE: spherical equivalent, ΔK: difference between flat and steep meridian, numbers: no. of eyes (%), WTR: with-the-rule astigmatism (negative cylinder axes are 180°±30°), ATR: against-the-rule astigmatism (negative cylinder axes are 90°±30°), OBL: oblique astigmatism (negative cylinder axes are over 30° - under 60° and over 120° - under 150°), NA: no astigmatism.
Refractive error^† (D)	Sph	−4.08±2.02 (−0.25 to −8.75)
	Cyl	−0.91±0.72 (0.00 to −3.50)
	SE	−4.53±2.04 (−1.38 to −9.25)
Keratometry (D)	Flat	42.44±1.12 (39.75 to 45.50)
	Steep	43.82±1.35 (41.00 to 47.25)
	ΔK	−1.38±0.72 (0.00 to −3.75)

Astigmatism	Refractive astigmatism^‡	Corneal astigmatism
†Based-spectacle. ‡Based-spectacle at vertex distance zero. SD: standard deviation, Sph: spherical power, Cyl: cylindrical power, SE: spherical equivalent, ΔK: difference between flat and steep meridian, numbers: no. of eyes (%), WTR: with-the-rule astigmatism (negative cylinder axes are 180°±30°), ATR: against-the-rule astigmatism (negative cylinder axes are 90°±30°), OBL: oblique astigmatism (negative cylinder axes are over 30° - under 60° and over 120° - under 150°), NA: no astigmatism.
WTR	125 (74.4)	161 (95.8)
ATR	10 (5.9)	3 (1.8)
OBL	7 (4.2)	3 (1.8)
NA	26 (15.5)	1 (0.6)

	Analysis of Javal’s rule by dioptric power matrix
	OJR	SJR	YRE	VJR
OJR: original Javal’s rule, SJR: simplified Javal’s rule, YRE: Yoo’s regression equation, VJR: vector-based Javal’s rule. †Different astigmatism (DA) between WTR and ATR. r: pearson correlation coefficient between the axes of corneal astigmatism and predicted refractive astigmatism. See other abbreviations and footnotes in Table 1.
WTR	147 (87.5)	135 (80.4)	124 (73.8)	153 (91.1)
ATR	11 (6.5)	9 (5.4)	22 (13.1)	4 (2.4)
OBL	10 (6.0)	22 (13.1)	22 (13.1)	11 (6.5)
NA	0 (0.0)	2 (1.2)	0 (0.0)	0 (0.0)
DA^†	6 (3.6)	3 (1.8)	5 (3.0)	6 (3.6)
r (between axes)	0.971 (p<0.001)	0.936 (p<0.001)	0.891 (p<0.001)	0.632 (p<0.001)

Between groups^†	Mean±SD (D) (p-value)^‡	r (p-value)	ICC (95% CI)	MD±SD (D)	95% LOA
†Reference: 0.82±0.65 D as the subjectively determined refractive astigmatism (SAt). ‡Paired t-test, SAt: subjectively determined refractive astigmatism SD: standard deviation, r: pearson’s correlation coefficient, ICC: intraclass correlation coefficient, CI: confidence interval, MD: mean difference, LOA: limits of agreement. See other abbreviations and footnotes in Table 1 and 2.
OJR vs. SAt	1.30±0.84 (p<0.001)	0.669 (p<0.001)	0.648 (0.551–0.728)	0.49±0.63	−0.75 to 1.72
SJR vs. SAt	0.97±0.66 (p<0.001)	0.662 (p<0.001)	0.662 (0.568–0.740)	0.15±0.54	−0.90 to 1.20
YRE vs. SAt	0.71±0.49 (p=0.004)	0.650 (p<0.001)	0.628 (0.526–0.711)	−0.11±0.50	−1.09 to 0.86
VJR vs. SAt	0.80±0.58 (p=0.662)	0.655 (p<0.001)	0.651 (0.555–0.730)	−0.02±0.51	−1.02 to 0.99

Magnitude		OJR	SJR	YRE	VJR
SAt: −0.06-0.70×179 as the subjectively determined refractive astigmatism, ΔAt: At – SAt. See other abbreviations and footnotes in Table 2.
At	Mean	−0.08-1.14×175	−0.08-0.81×175	−0.09-0.53×174	−0.04-0.71×177
ΔAt	Mean	−0.02-0.45×170	0.00-0.15×156	+0.15-0.20×102	+0.02-0.03×141
	≤ 0.25 D	21 (12.5)	33 (19.6)	43 (25.6)	48 (28.6)
	≤ 0.50 D	56 (33.3)	94 (56.0)	100 (59.5)	103 (61.3)
	≤ 0.75 D	95 (56.5)	133 (79.2)	134 (79.8)	135 (80.4)
	≤ 1.00 D	131 (78.0)	152 (90.5)	147 (87.5)	150 (89.3)
	≤ 1.50 D	158 (94.0)	163 (97.0)	165 (98.2)	162 (96.4)
	≤ 2.00 D	164 (97.6)	165 (98.2)	167 (99.4)	165 (98.2)
	>2.00 D	4 (2.4)	3 (1.8)	1 (0.6)	3 (1.8)