조절반응을 이용한 노안 근용가입도 결정 방법

1. 대상

2020년 1월에서 5월까지 약 5개월 동안, 경기도 양주시에 거주하는 주민을 대상으로 사전에 충분한 설명과 함께 동의를 받아 신체의 변화를 초래하지 않는 비 접촉방식의 측정장비(retinoscope, no 18235, welchallyn, USA)로 근거리 가입도 임계점을 구하기 위하여 검영법을 실시하였다.

연구대상자는 단안 맹이거나, 각막 절삭술 환자, 백내장 환자, 순환기 내과 질환인 당뇨나 고혈압 그리고 가성근시자(pseudomyopia) 등 통계적 오류를 일으키는 대상자는 제외하였다. 그리고 중심와 반사(foveal reflex)가 좋은 대상자 중 근시자 130명(남 72명, 여 58명)과 원시자 60명(남 32명, 여 28명)으로 잠복원시자(latent hyperopia)를 포함해서 총 190명을 선정하였다. 그리고 검사 대상자 중 결측치는 없으며 인구통계학적 빈도분석 결과는 다음과 같다.

근시자 평균은 35.19±1.43세이고 중위수(median)는 33세이며, 남성과 여성은 각각 55.4%, 44.6%이다. 그리고 연령별 분포를 보면 29.20%(20~29세)>18.50%(40~49세)=18.50%(50~59세)>16.90%(10~19세)>10.80%(30~39세)>6.20%(60~69세) 순이다.

노안 근용가입도 산출을 위한 모형이므로 40대 미만의 선천성 원시자(congenital hyperopia)를 제외한 연령 증가에 따른 40대 이상 원시자의 평균은 61.73±1.13세, 중위수는 62세이고 남성과 여성은 각각 53.30%, 46.70%이며, 연령대는 65.00%(60~69세)>28.30%(50~59세)>6.70%(40~49세) 순이다. 각 연령에 따른 인구통계학적 분포에서 근시는 왜도(skewness) 0.22±0.21, 첨도(kurtosis) −1.98±0.42이며, 원시는 왜도 0.14±0.31, 첨도 –2.05±0.61이다. 왜도는 근시 및 원시 모두 절대치 ±3.00 이상과 첨도가 8~20 사이 값이 아니므로 정규성 분포를 이루고 있다(Table 1).

Table 1.

Frequency analysis of participant demographics

2. 연구모형 및 과제

매개변수인 원점 조절반응(△AR_f)을 중심으로, 조절반응진폭(△AMP)을 독립변수로 놓고, 근점 조절반응(△AR_n)과 가입도(△ADD) 변수를 종속변수로 하여 다음과 같은 연구과제를 선정하였다.

H_-1. 독립변수인 근점 조절반응(AR_n)과 종속변수인 조절반응진폭(AMP)과 가입도(ADD) 사이에 원점 조절반응(AR_f)의 매개효과 검정과 노안 근용가입도 산출을 위한 임계점의 유의성 해석.

H_-2. 조절반응(AR_f)을 매개효과로 하여 근점 조절반응(AR_n)과 종속변수인 조절반응진폭(AMP) 그리고 가입도(ADD) 사이에 영향관계와 가입도 임계점을 이용한 노안 근용가입도 산출식의 유의성 해석.

3. 측정장비

본 연구는 안와 내 가입도에 영향을 미치는 변수들의 정량적 크기를 정의하기 위해서 검영기를 사용하여 MEM(monocular estimate method)검사법을 이용하여 조절인자에 관련된 측정 변수값을 구하기 위해서 스넬린(snellen chart) E 단일문자와 결합된 검영기(no. 18235, welchallyn, USA)와 5단 판부렌즈(tmi-3, hata’s retinoscope lens set 5 bar, Japan)의 굴절검사 기기를 이용하였다.^[7] 그리고 고정 자극점(stimulus point)은 근거리 0.33 m 및 원거리 3 m 시표를 사용하였고, 검사실의 조도는 50 lx 및 원거리 시표는 200 lx를 사용하였다.

4. 변수의 정의 및 방법

단안의 각막을 정점을 기준으로 각막 외부의 원점에서부터 근점까지 자극에 대응하는 안와 내 반응의 범위는 시축의 절대좌표와 이를 응용한 보조좌표를 이용하였다. 시축의 절대좌표에서 망막을 기준으로 후면은 근점에 대한 조절반응은 + Diopter로 표시 하였고, 망막의 전면은 원점에 대한 조절반응으로 - Diopter로 표시 하였다. 그리고 Fig. 2와 같이 시축의 좌표에서 조절반응범위를 구하기 위해서 안와 외 근점 자극에 대한 안와 내 조절반응점(AR_n)은 시축에서 하측의 절대좌표(AR_n Axis)를 사용하였고, 안와 외 원점 자극에 대한 안와 내 조절반응점(AR_f)의 좌표는 시축에서 상측의 보조좌표(AR_f Axis)를 사용하였다. 그리고 절대좌표와 보조좌표의 차가 항상 ±3.00 D의 차이는 검영기 버전스 값이 항상 0.33 m을 기준으로 하였기 때문이다.

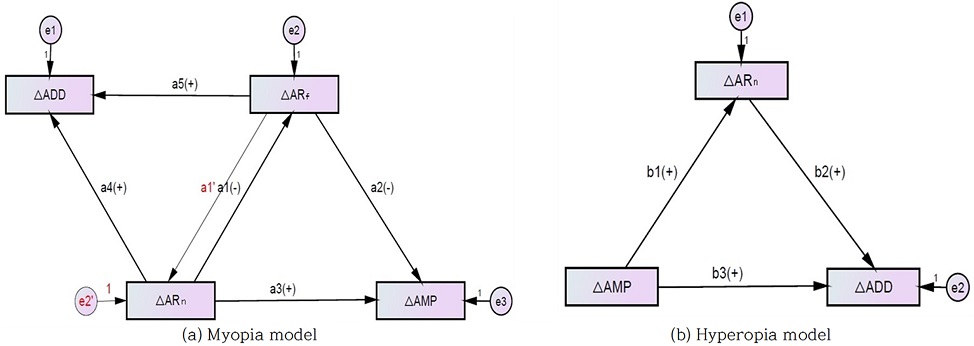
Fig. 1에서 각각 연구모형을 구성하는 변수는, 근시모형에서 단안의 자극에 대응하는 동공반사(pupil reflection)를 이용한 조절반응진폭(AMP), 근점 조절반응(AR_n), 원점 조절반응(AR_f) 그리고 근점 조절반응 내 임계점(critical point)을 기준으로 측정된 가입도(ADD)를 포함해서 4개의 조절인자로 구성하였다. Sarah Hinkley의 18세 미만의 미성년자를 대상자의 조절지연에 관련된 보고서에서 정시를 포함한 굴절이상 안의 대부분 +0.50~+0.75 D의 조절지체(stimulus: 0.40 m)가 있어, 이것은 양(+) 아닌 음(–)의 조절지체로 이해되어야 하며 원점 조절반응(–)과 무관하지 않다.^[18] 연령의 증가에 따른 원시모형에서 망막에 완전교정을 할 경우, 원점 조절반응(–)의 폭은 거의 소멸에 가깝게 작아지는 데 비하여, 근거리 시력에 대한 조절지체는 증가에도 불구하고 근점 조절반응(+)의 증가로 인하여 원점 조절반응을 제외한 나머지 3개의 조절인자(조절반응진폭, 근점 조절반응, 가입도)로 모형을 구성하였고 조절인자들의 정의와 측정방법은 다음과 같다.

Fig. 1.

Myopia model and hyperopia model.

단안의 조절반응점 간의 범위(the range of accommodative response corresponding from the far point in space to the near point: AMP)는 동적 검영법을 이용한 것으로 안와 내 시축에서 단안의 조절휴지상태(3.00 m 이상)에 대응하는 원점 조절반응점(AR_f)에서 근점(0.33 m)에 대응하는 안와 내 근점 조절반응점(AR_n)까지 범위의 합(±)을 의미하며 단안 시력교정의 기준이 된다. 각막 정점을 기준으로 안경 교정후 자극에 대응하는 안와 내 조절반응의 범위가 단안마다 동일하거나 그렇지 않기 때문에 ‘단안 조절반응의 고유진폭(natural amplitude)’으로 해석되어 단안의 외부 자극(0.33~3.00 m)에 대한 안와 내 조절반응점 사이의 범위(AR_f~AR_n)를 조절반응진폭(AMP)이라 정의하였다.

조절반응진폭은 단안 내 조절의 특성을 잘 설명해 주며, 연령의 증가 및 안와 내 구조물의 변화에 따른 보상적 변화 등 여러 가지 원인으로 동일하지 않은 경우가 근시모형(N=130)에서 42.30%, 원시모형(N=60)에서 30.00%의 비율을 보였다. 교정하지 않은 나안상태에서 단안의 조절반응진폭을 구하는 임상식은 ‘AMP=(3-원거리굴절도)+근거리굴절도’의 실험식을 이용하여 조절반응점 사이의 범위(AMP)를 구했다(Table 3, 5).^[8]

Table 2.

Comparison analysis of the model fit of myopia and hyperopia models

Table 3.

Parameter evaluation of the main variables scale: Diopter

원거리 자극에 대응하는 조절반응(accommodative response corresponding to the far point: AR_f)은 근점 조절반응(AR_n)과 조절반응진폭(AMP)의 차(AR_f=AR_n−AMP)로서 잔류굴절오차(the residual refractive error)를 의미한다.^[9] 그리고 조절폭주를 동반하지 않는 원점 거리에 대한 반응값(−)을 말하며 근시진행과는 상관관계가 유의하지 않다는 보고가 있다.^[10] 측정 방법은 단안의 나안 상태에서 3.00 m이상(조절휴지상태)의 안와 외 원점 자극에 대응하는 굴절교정 전의 원점 조절반응점(blur point)이며, 단안의 조절반응진폭의 조건에 따른 ±0.25 D 단계로 가감하여 원방시 교정후의 원점 조절반응점(AR_f)을 기준으로 하였다. 근점 조절반응은 황반부 중심와를 시축상의 절대좌표의 0.00을 기준으로 한다면, 원점 조절반응점은 안와 외 자극을 –3.00 D (1/0.33 m)을 원인으로 하여 절대좌표를 응용하여 ±3.00 D 차이를 보이는 보조좌표(원점: 절대좌표의 –3.00 D 지점)를 이용하였다. 한편 연령이 증가에 의한 원시안은 원점 조절반응량(−)이 존재하지 않다고 가정하고 완전교정을 하기 때문에 부(−)의 영향관계에 있는 근점 조절반응량(+)이 증가하여 조절지체의 원인이 된다. 따라서 본 연구에서 연령의 증가에 따른 원시모형에서 근거리에 대한 근점 조절지체(+)가 증가하고 반대로 원거리에 대한 원점 조절지체(−)는 감소한 것으로 보고, 황반부 중심와에 완전교정한 값을 기준으로 하였다(Fig. 2).^[11]

Fig. 2.

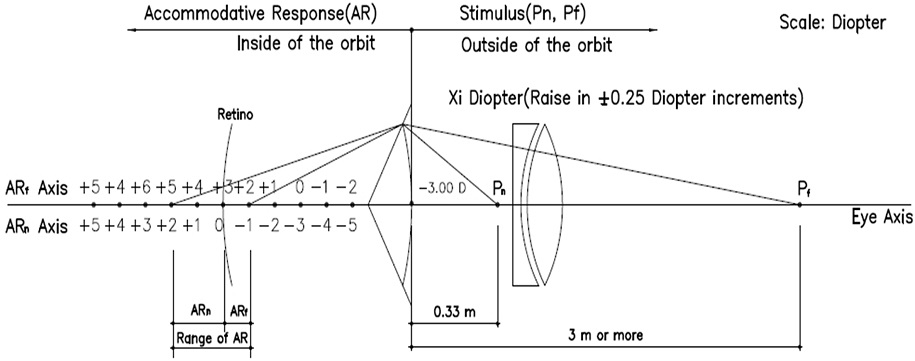
Techniques methods to find points accommodative response of the par point, accommodative response of the near point accommodative and the range of accommodative response corresponding from the far point in space to the near point corresponding to external stimulus in the monocular.

근거리 자극에 대응하는 조절반응(accommodative response corresponding to the near point: AR_n)은 망막 황반부 중심와를 기준점으로 한 절대좌표에서 근점거리(0.33 m)에 대응하는 검영기의 반사점(break point)을 구한 값이다.^[12] 측정 방법은 원점 조절반응을 –1.00 D 기준으로 원거리 시력교정 후 단안의 조절반응진폭의 특성에 따른 ±0.25 D 가감하여 추가적인 굴절교정 후, 시축 망막 후면부 반응범위를 근점 조절반응으로 하였다. 그리고 연령의 증가에 따른 조절반응 변동(fluctuations of the accommodative response)이 점차적으로 감소함에 따라 + 굴절 가입도는 증가를 하여 시축의 망막에서 조절반응의 굴절도는 커진다.^[13] 원거리 시력 굴절교정상태에서 검영기의 MEM 검사에서 근점 자극에 대한 반응으로 시축에서 망막을 경계로 하여 절대좌표의 후면부(+)의 한 지점에 해당되며 교정 후 항상 양(+)의 값을 가진다. 그리고 원점조절반응(AR_f)과 구분하기 위해서 ‘AR_n’로 표시 하였다.

가입도(addition)는 단안에서 외부자극(0.33m)에 대한 ‘근점 조절반응−근점 조절반응 내 임계점’을 처방 후 문진에 의해서 확인하였다.^[14] 임상결과에 의하면 근시모형에서는 연령의 증가에 따른 원점 조절반응의 연령별 평균 변화는 유의하지 않았고, 조절반응진폭의 변화에 따른 근점 조절반응 내 임계점(critical point)의 변화의 원인이 되어 가입도가 증가되었다(Table 4). 완전교정한 원시안에서는 비교적 일정한 기준 임계값(+1.00 D)을 가지며, 잠복원시안은 잠복원시의 편차만큼 가입도가 증가 될 수 있다는 점에 주의해야 한다(Fig. 1).

Table 4.

Analysis of the mean accommodative response in the myopia and hyperopia models as a function of age scale: Diopter

5. 분석방법

조절반응진폭이 3.25 D를 넘는 경우 근점 조절반응의 차이를 확인하기 위해서 추가 교정을 하지 않은 조건의 근시모형은 △AMP, △AR_f, △AR_n 그리고 △ADD를 포함한 4개의 변수를 이용하였고, 근점 조절반응의 차이를 확인하기 위해서 잠복원시를 교정하지 않은 조건에서 원시모형은 원점 조절반응을 제외한 △AMP, △AR_n 그리고 △ADD를 포함한 3개의 변수를 이용하여 SPSS(statistical package for social sciences, ver. 21)에서 단안별로 각각 원시 데이터로 코딩하였다. 그리고 양안의 특성을 적용하기 위해, 양안의 조절반응 중에서 ±2.75~±3.00 D에 근접한 단안을 기준안(dominant eye)으로 하고, 양안의 보상적 변화의 특성을 반영하기 위해서 편차(dominant value–recessive value)를 이용하였다.

조절반응진폭의 편차를 △AMP, 근점 조절반응의 편차를 △AR_n, 원점 조절반응의 편차를 △AR_f 그리고 가입도의 편차를 △ADD(이하 조절반응진폭, 근점 조절반응, 원점 조절반응, 가입도라 한다)로 하여 양안의 특성을 잘 나타내도록 하였다. 그리고 안와 내 조절과 관련된 변수 간의 연관성이 높은 관계로 다중공선성(multicollinearity)을 방지하기 위해 평균 중심화(mean centering)를 하였다.

AMOS(analysis of moment structure, ver. 21)을 이용하여 다변량 구조방정식 모형(multivariate structure equation modeling)으로 각 모형적합도(model fit)를 확인하였고, 변수 간의 상대효과를 파악하기 위해서 제약(a_n=b_n) 및 비제약모델(a_n≠b_n)을 이용하여 상대적 효과를 검정하였다. 그리고 각 모형의 직접효과(direct effects)는 변수 간의 영향관계 및 간접효과(indirect effects)는 원점 조절반응의 매개효과 그리고 총효과(total effects)의 영향관계를 확인하여 가입도 기준인 근점 조절반응 내 임계점을 기준으로 노안 근용가입도 산출식을 검정하였다.

1. 연구모형의 적합도 평가

Fig. 1 Myopia model과 Fig. 2 Hyperopia model을 연구모형로 하여 AMOS의 지수를 확인하여 데이터가 연구모형을 잘 반영하는지 모델적합도(model fit) 평가를 하였다.

근시안의 경우, 매개변수인 원점 조절반응을 포함하여 총 4개의 변수로 구성된 연구모형(default model)에서 연구모형이 입력자료를 설명하는 정도의 절대 적합도를 살펴보면, 모형이 귀무가설이 아닌 연구가설(p=0.031<0.05)이며, 표준카이제곱(normed chi-square: CMIN/DF)이 4.63>3.84로 낮지만, RMR(root mean square residual)지수는 0.00<0.05, GFI(goodness of fit index)지수는 0.98>0.90로 데이터가 모형을 잘 설명을 하고 있다. 그리고 연구모형이 null 모형대비 적합도를 나타내는 대표적인 지수인 증분적합도 CFI(comparative fit index) 지수는 0.99>0.90로 수용가능한 적합지수를 보인다. 이와 달리 완전교정된 원시안의 경우 근점 조절반응을 매개변수로 총 3개의 변수로 구성된 모형으로 적합도를 살펴보면, 자유도(DF) 및 CMIN(χ²)이 0으로, 모델적합도가 필요가 없고 변수 간의 영향관계만 확인하는 포화모형(saturated model)이다(Table 2).

2. 주요 변수의 모수평가

연령증가에 따른 안와 내 구조물의 변화는 10대에서 가장 적고, 10~20대까지 안와 골격이 성장을 하여 40~50대에서 높게 측정이 되었다.^[15] 그리고 정시안에서 연령에 따른 안수치의 변화의 보고서에서 안축장의 변화에 따른 각막곡률반경, 유리체 깊이 그리고 안축장은 평균 25세를 기점으로 감소양상을 보이면서 유의한 보상적 변화를 보였다.^[16] 또한 굴절도에 따른 안축장과 전방깊이의 상관관계에서 정시안의 평균 안축장은 23.94 mm이고 평균 전방 깊이는 평균 3.08 mm인데 비해 –3.00 D 이상 굴절도에서 –1.00 D 증가시 안축장은 0.29 mm, 전방깊이는 0.08 mm 유의하게 증가하였다.^[17]

연령의 증가로 안축장의 변화를 원인으로 하는 굴절변화에 대응한 보상적 변화로 외부 자극에 대응하는 단안의 고유한 조절반응진폭의 범위(이하 조절반응진폭이라 한다)를 가진다. 근시 및 원시모형에서 40대까지는 연령의 증가에 따른 조절반응진폭에서 유의한 변화가 없었고, 50대 전·후에서 근점 조절반응에서 유의한 변화를 보인 것은 조절지체가 근점 조절반응이 원인인 것으로 보인다(Table 4).

50대 전·후 근시안에서 피로도가 증가하고, 정시안의 경우 원시안으로 진행을 하여 가입도가 필요하다. 따라서 조절반응의 변화를 원인으로 하여 모델적합도가 상이하여 근시 및 원시모형으로 별도 분리하여 조절변수의 모수 평가할 필요성이 있다.

근점의 자극(0.33 m)에 대응하는 안와 내 망막 후면부의 시축상 절대좌표의 반응값으로 가입도에 직접적인 영향을 미치는 근거리 자극에 대한 조절반응(AR_n)은 연령의 증가에 따른 원점 조절반응과 부(−)의 영향관계를 가지며, 이 두 반응의 범위의 합인 단안 조절반응진폭의 양안 오차범위에 따라 정상에 해당하는 I군(±0.00~±0.25 D)과 양안시가 필요로 하는 II군(±0.5~±0.75 D) 그리고 시기능 운동이 필요한 III군(±1.00 D 이상)으로 구분하였고, I군은 57.70%, II군은 33.80% 그리고 III군은 8.50%의 차이를 보였다. 양안이 동일하지 않은 경우는 모집단의 조절지연 보고서(stimumus: 40 cm, Nott Retinoscopy)에서 근시 및 정시에서도 대부분 +0.50~+0.75 D의 조절지연이 있다는 것은, 원점 조절반응이 정상 범위 내 조절지연(−)과 상관관계가 있다는 것으로 이해된다(Table 5).^[18]

Table 5.

Analysis of the mean difference in monocular △AMP between the two models

근시모형에서 우안의 평균 조절반응진폭(AMP)은 ±2.80±0.04 D, 좌안은 ±2.77±0.03 D, 중위수(median)와 최빈값(mode)은 ±3.00 D로 동일하다. 양안 조절반응진폭의 범위는 ±2.13~±3.38 D로, 평균은 ±2.78±0.03 D이며 중위수는 ±2.75 D이고 최빈값은 ±3.00 D이다. 따라서 근시안에서 좌안과 우안의 평균차는 +0.03±0.00 D로 근사치며, 중위수와 최빈값은 차이가 없다.

근점 조절반응(AR_n)의 우안 평균값은 1.95±0.02 D, 좌안은 1.94±0.02 D이고, 중위수와 최빈값은 2.00 D로 동일하다. 그리고 양안 조절력의 최소~최대값 범위는 +1.50~+2.50 D로 평균 ‘1.95±0.02 D’이다.

굴절에 영향을 미치는 조절인자들 사이의 매개변수이자 판별타당도에 영향을 미치는 원거리 자극에 대한 조절반응(AR_f)은 Fig. 2의 절대좌표를 기준으로 항상 음(−)의 값으로 우안의 평균값은 –0.84±0.02 D, 좌안은 –0.83±0.02 D이며, 중위수와 최빈값은 –1.00 D로 동일하다. 그리고 양안의 원점 조절반응점의 범위는 –0.25~−1.25 D이고, 평균 –0.84±0.02 D이며, 중위수는 –0.88 D 그리고 최빈값은 –1.00 D이다.

조절변수의 모수 평가에서 특이한 것은 양안의 원점 조절반응의 중위수와 최빈값이 –1.00 D일 때, 안와 내 조절반응진폭의 중위수가 ±2.75 D이고 최빈값은 ±3.00 D이다. 근점 조절반응의 중위수와 최빈값이 2.00 D이라는 것은, 안경 굴절검사에 있어서 근시안의 최적시력의 교정 후 근점 조절반응점 2.00 D는 가입도 검사에 기준점(critical point)이라는 것을 의미한다.

한편, 원시모형 조절반응진폭(AMP)의 경우 우안의 평균값은 ±3.05±0.04 D, 좌안은 ±2.91±0.05 D이고, 양안 조절반응진폭의 범위는 ±2.50~±3.88 D로 평균 ±2.98±0.03 D이며, 중위수 및 최빈값이 3.00 D이다.

원시모형에서 근거리 자극에 대한 평균 조절반응(AR_n)의 경우 우안은 2.90±0.05 D, 좌안은 3.03±0.05 D이고, 양안에서 조절진폭의 범위는 ±2.38~±3.88 D에서 평균 ±2.97±0.03 D로 중위수 및 최빈값이 3.00 D이다.

조절반응진폭와 근점 조절반응 사이의 매개역할을 하는 원거리 자극에 대한 조절반응(AR_f)의 경우, 우안의 평균값은 –0.01±0.05 D이며, 좌안은 –0.02±0.01 D이다. 그리고 양안의 평균은 –0.01±0.06 D로 유의하지 않았고, 안와 내 조절반응진폭의 평균값과 근거리 자극에 대한 조절반응의 평균값이 유사한 것은 연령에 증가에 따라 근시안을 제외한 정시나 원시에서 정상범위의 조절지연은 소멸하고 근거리에 관련된 조절지연은 증가하기 때문인 것으로 판단된다(Table 3).

3. 변수들 간의 직접효과와 다중상관제곱

Table 6은 변수 간의 직접효과(direct effect)를 나타낸 값이며, Table 7의 다중상관제곱값(squared multiple correlations: SMC)은 독립변수가 종속변수를 설명하는 정도(R²)를 나타내며, 근시모형에서 원점 조절반응(AR_f)의 다중상관제곱값은 변수 간의 판별성(discriminant validity)을 높여 모델적합도(model fit)를 높이는 원인이 된다.

Table 6.

Regression weights in the myopia and hyperopia models: direct effects

Table 7.

Squared multiple correlations of the myopia and hyperopia models: R2

근시모형에서 매개역할을 하는 원점 조절반응(AR_f)을 포함해서 근점 조절반응(AR_n), 조절반응진폭(AMP) 그리고 가입도(ADD)의 영향관계를 보면, 경로 a1(△AR_f←△AR_n)와 a2(△AMP←△AR_f)는 부(−)의 영향 관계에 있고, 나머지 변수 간의 관계는 정(+)의 영향 관계에 있다(Fig. 1).

경로 간 영향관계(direct effect)를 살펴보면, AR_f를 매개변수로 한 경로 a1(−), a2(−), a3(+)에서 매개변수인 AR_f와 독립변수인 AR_n는 부(−)의 영향관계로 ±2.75 D≤AMP≤±3.00 D의 경우 AR_n 반응량은 유의한 변화가 없었고, ±1.00 D≤AMP≤±2.50 D의 조건에서 원방시 굴절교정을 위해 - Diopter를 증가한 경우 안와 내 조절인자의 보상적 변화로 안와 내 시축에서 망막을 기준으로 AR_f 반응점(−)은 좁아지면서 AR_n 반응점(+)은 커진다. 그리고 독립변수인 AR_n는 종속변수인 AMP와 정(+)의 영향관계로 연령에 따른 조절지체가 증가하여 AMP도 정(+)의 방향으로 증가를 하게 된다(Table 4, 6).

일반적으로 ±2.75 D≤AMP≤±3.00 D의 정상적인 조절반응진폭의 범위 내에서 AR_n 반응량은 유의한 변화를 보이지 않으나, AMP≥±2.50 D의 조건에서 매개변수 AR_f는 종속변수 AMP와 부(−)의 영향을 미치기 때문에 원거리시력의 굴절가입도가 – Diopter 가입량 만큼, 시축상의 망막을 기준으로 AR_f 반응점이 줄면서 AR_n 반응량이 증가를 하여 정(+)의 방향으로 영향을 미치는 AMP는 증가된다. 그리고 경로 a3(△AMP←△AR_n)의 비 표준화 계수(factor loading)가 1.31±0.04로 정(+)의 영향을 미칠 때, 경로 a1(△AR_f←△AR_n) 및 a2(△AMP←△AR_f)에서 변수가 서로 부(−)의 영향을 미치는 것은 매개변수인 AR_f은 변수 간의 길항작용을 하기 때문이다.

한편, AR_f를 매개변수로 한 경로 a1(−), a4(+), a5(+)에서 매개변수인 AR_f은 종속변수인 ADD와 정(+)의 관계에 있다. ±1.00≤AMP≤±3.00 D 조건에서 AR_f의 반응범위가 좁아지면 AR_n의 반응범위가 늘어나 ADD가 일정하게 증가를 하였지만, AMP≥±3.25 D의 조건에서는 AR_f가 시축상의 망막을 경계로 반응점이 증가하면서 근거리 조절지체로 ADD는 유의할 정도로 높아져서 다른 패턴을 보이고 있기 때문에 Fig. 1의 근시모형(a)은 ±1.00≤AMP≤±3.00 D의 조건을 만족하여야 한다. 또한 독립변수인 AR_n은 종속변수인 ADD에 정(+)의 방향으로 영향을 미치는 것은 AR_n의 AMP와 정(+)의 영향관계에 있고 Table 4에서 연령증가에 따른 AMP의 증가는 결국 ADD에 정(+)의 영향을 주기 때문이다(Table 4, 6).

원시모형을 구성하는 주요 굴절인자는 AR_f을 제외한 AR_n을 매개변수로 하여 독립변수는 AMP이고 종속변수는 ADD로 구성되며 각 변수 간 정(+)의 방향으로 유의하다(Table 6).

두 모형에서 다중상관제곱를 확인해 보면, 근시모형에서 AR_f이 존재함으로써(0.05) 모델의 간명성으로 구분할 때 변수들 간의 판별타당도를 높여 모델적합도에 기여한다. 따라서 AR_f은 다른 조절인자 간의 판별성을 높이는 주요 변수가 되며, AR_f을 제외한 완전교정 된 원시안에서는 판별타당도가 낮아 모형을 구성하는 변수들 간의 상관관계가 매우 높아 포화모델이 된다(Table 7).

4. 변수들 간의 매개효과와 총효과 분석

가입도 산출은 Fig. 1(a)의 근시모형에서 독립변수인 AR_n 과 종속변수인 AMP 그리고 매개변수인 AR_f 간의 영향관계에 의해서 결정되는 단안의 가입도를 추정하기 위해서 변수 간의 영향관계를 확인할 필요가 있다. 각 변수들을 대상으로 양안의 단안차(dominant value-recessive value)를 이용하여 양안의 특성을 살리고, 평균중심화를 이용한 표준화된 변수들(△AMP, △AR_n, △AR_f, △ADD)을 다변량 구조방정식 모형에 대한 양안의 직접 및 간접 그리고 총효과의 영향 관계를 확인하였다.

Fig. 1의 직접효과는 Table 6이고, 변수 간 매개효과를 검정하기 위한 간접효과는 Table 8이며, 총효과(직접효과+간접효과)는 Table 9이다. 그리고 각 Table의 횡 방향(lateral direction)은 독립변수이며 종 방향(longitudinal direction)은 종속변수를 나타낸다.

Table 8.

Indirect effects (standardized indirect effects) of the unconstrained model (an≠bn)

Table 9.

Total effects (standardized indirect effects) of the unconstrained model (an≠bn)

Fig. 1과 Table 6, 8에서 직접 및 간접효과 영향 관계를 살펴보면, 근시모형에서 △AR_f를 매개변수로 하여 경로 a3(△AMP←△AR_n)에서 독립변수인 AR_n은 종속변수인 AMP에 직접효과와 AR_f을 매개변수로 한 간접효과 모두 정(+) 영향력을 미치기 때문에 AR_n와 AR_f은 AMP에 영향을 미치고 있다. 그리고 경로 a4(△ADD←△AR_n)는 독립변수인 AR_n은 종속변수인 ADD에 정(+)의 영향을 미쳤지만, AR_f을 매개변수로 한 간접효과에는 부(−)의 영향을 미치기 때문에 AR_n은 ADD에 직접적인 영향력이 크다고 할 수 있다.

Table 9의 총효과에서 경로 a3의 총효과는 △AR_f를 매개변수로 하는 정(+)의 간접효과를 포함하고, 경로 a4의 총효과는 부(−)의 간접효과를 포함한다. 따라서 단안의 AMP가 일정하다면, 간접효과에 의해서 경로 a3의 총효과는 직접효과 보다 0.16의 큰 값을 가지며, 경로 a4의 총효과는 직접효과 보다 –0.17의 작은 값을 가진다(Table 6, 8, 9)(Fig. 1).

5. 변수들 간의 회귀곡선 추정

Fig. 3은 근시모형에서 변수 간의 회귀곡선 추정이며, Fig. 4는 잠복원시(latent hyperopia)를 교정하지 않은 원시모형에서 변수 간의 영향 관계를 나타낸 것이다. 잠복원시를 교정하지 않은 이유는 잠복원시를 교정할 경우 AR_n의 변화량의 차이를 확인이 어렵기 때문이다.

FIg. 3.

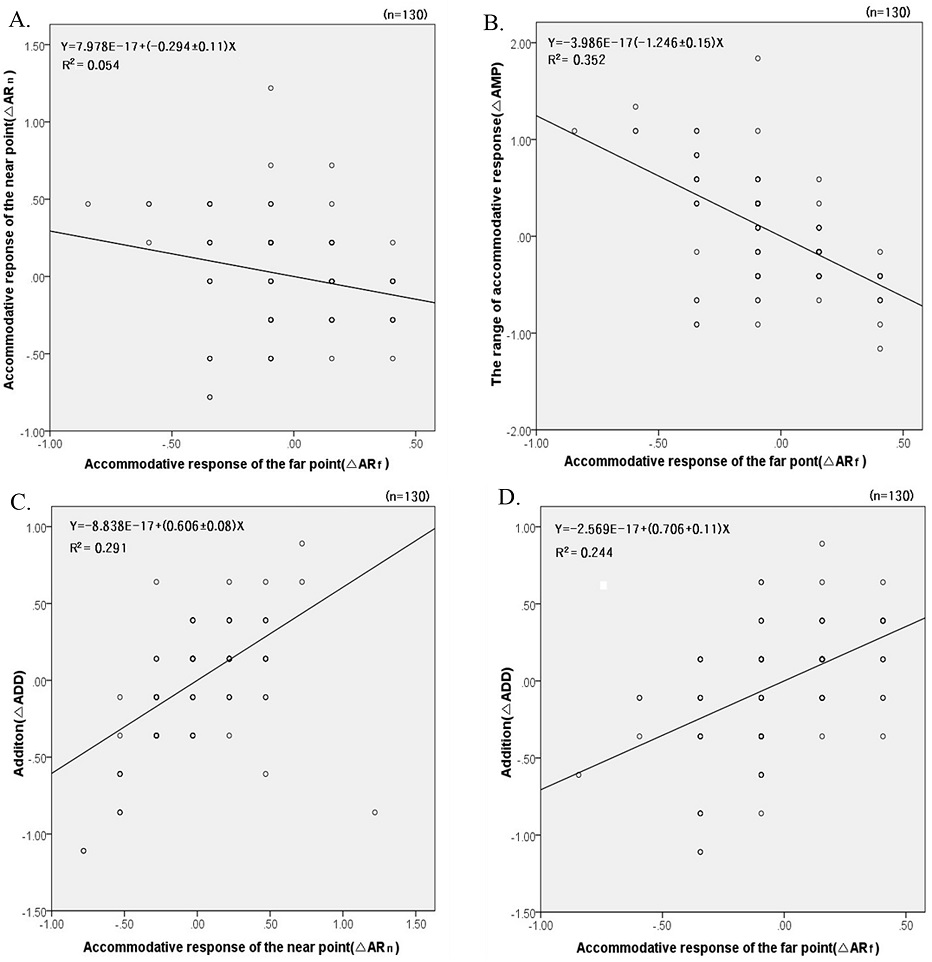
Estimated curves of △AMP, △ARf, △ARn and △ADD in the myopia model. A. △ARn←△ARf, B.△AMP←△ARf, C. △ADD←△ARn, D. △ADD←△ARf.

Fig. 4.

Estimated curves of △AMP, △ARn, and △ADD in the hyperopia model. A.△ADD←△ARn, B.△ADD←△AMP.

Fig. 3은 Fig. 1(a)의 근시모형에서 △AR_n를 매개변수로 하고 독립변수인 △AR_f와 종속변수인 △ △AMP로 경로 수정된 근시모형의 영향 관계를 살펴보면, 경로 a1′(△AR_n←△AR_f)와 a2(△AMP←△AR_f)에서 AMOS을 이용한 회귀분석에서 직접효과는 a1′(−0.29±0.11)<a2(−0.86±0.05)의 결과를 보여 주었다. 그리고 △AR_n←△AR_f 간의 비표준회귀식은 Y=7.978E−17+(−0.294±0.11)χ이고, △AMP←△AR_f 간의 비표준 회귀식은 Y=−3.986E−17+(−1.246±0.15)χ의 추정곡선 기울기를 보여주고 있다. 따라서 Fig. 3(a)의 경로 a1′ 및 a2의 직접효과 및 독립변수와 종속변수 간의 추정곡선 기울기를 비교해볼 때 AR_f가 AR_n보다 AMP에 부(−)의 방향으로 더 큰 영향을 미치는 것으로 나타났다(a1′<a2)(Fig. 3). 그리고 △AR_f를 매개변수로 하고 독립변수인 △AR_n과 종속변수인 △ADD의 영향 관계를 살펴보면, 경로 a4(△ADD←△AR_n)의 직접효과는 0.78±0.06이며, 경로 a5(△ADD←△AR_f)의 직접효과는 0.93±0.07로 AMP≥±3.25 D의 조건에서 추가 교정하지 않을 경우 a4<a5의 결과를 보여 주었다. 그리고 △ADD←△AR_n 간의 비표준화 회귀식은 Y=−8.838E−17+(0.606±0.08)χ이다. △ADD←△AR_f 간의 비표준화 회귀식은 Y=−2.569E−17+(0.706±0.11)χ로 두 경로 간의 원점 조절반응보다 근점 조절반응의 시각적 곡선기울기가 다소 높게 나타나는 것은 상수값이 큰 것이 원인이다. 이는 AMP≥±3.25 D의 조건에서 원거리 시력을 위한 안경굴절교정 후 AMP>±3.00 D을 넘는 잔류굴절오차에 대해서 추가 교정이 필요하기 때문이다(a4>a5)(Fig. 1, 3).

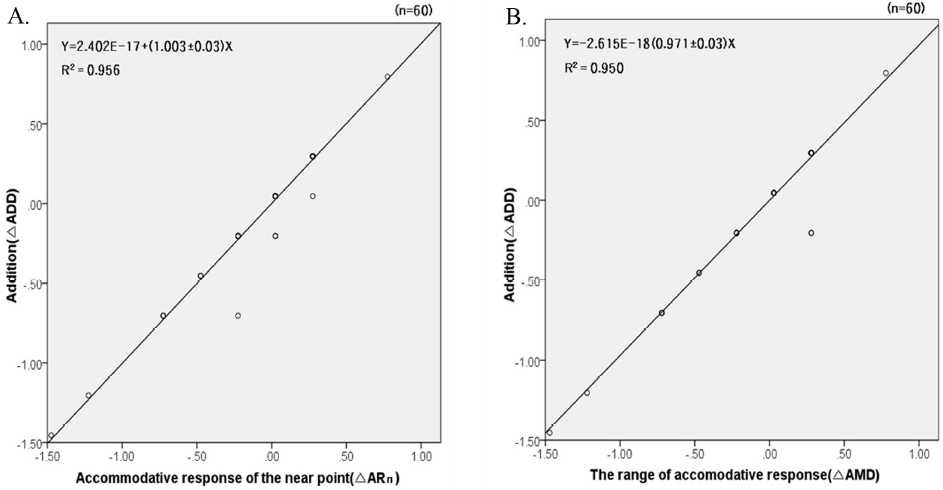
한편, 잠복원시를 교정하지 않은 Fig. 1(b)의 원시모형에서 △AR_n를 매개변수로 하는 독립변수 △AMP와 그리고 종속변수 △ADD 사이의 영향관계를 살펴보면, 경로 b2(△ADD←△AR_n)의 직접효과는 0.58±0.12이고, 경로 b3(△ADD←△AMP)의 직접효과는 0.42±0.11로 거의 유사한 결과를 나타낸다. 그리고 △ADD←△AR_n 간의 비표준 회귀식은 Y=2.402E−17+(1.003±0.03)χ이고, △ADD←△AMD 간의 비표준화 회귀식은 Y=−2.615E−18+(0.971±0.03)χ로 기울기가 유사한 것은 단안 내 시축상의 AR_n와 AMP가 유사함을 말한다(b2≑b3)(Fig. 4).

6. 경로계수 간의 상대적 효과분석

근시 및 원시모형에서 경로계수 간 영향관계는 직접효과와 회귀곡선을 통해 확인이 가능하여도, 다중 회귀분석에서 경로 간 상대적 효과에 대해서 확인할 필요성이 있다. 따라서 비제약모델(unconstrained model: a_n≠b_n)을 디폴트값으로 놓고, 제약모델(constrained model: a_n≠b_n)의 변수제약(parameter constraints)을 이용하여 절대적합도 지수인 3.84/1(CMIN/DF)과 귀무가설(p>0.05)을 기준으로 변수 간의 상대적 유의성 평가를 확인하면 다음과 같은 결과가 도출된다.

Fig. 1(a)에서 근시모형의 수정된 경로 a1′(△AR_n←△AR_f)과 a2(△AMP←△AR_f)에서 경로 간 유의한 차이를 확인하기 위해서, 비제약모델(a1′≠a2)을 디폴트모델로 놓고, 제약모델(a1′=a2)을 분석한 결과 21.80/1>3.87/1(CMIN/DF) 및 0.00<0.05(연구가설)로 제약모델보다 비제약모델이 우수하여 경로계수 간의 차이가 있음을 통계적으로 유의하게 나타났다. 동일 방법으로 경로 a4(△ADD←△AR_n)와 a5(△ADD←△AR_f)의 경로 간 차이가 유의한 수준인지를 확인해 보면, 3.87/1>3.84/1 및 0.049<0.05(연구가설)로 제약모델보다 비제약모델이 우수하여 두 경로 간 차이가 있는 것으로 나타났다. 한편 Fig. 1(b)의 △AR_n을 매개변수로 하는 원시모형에서 경로 b1과 b3 간에 0.52/1<3.84/1 및 0.47>0.05(귀무가설)을 수용하여 제약모델이 우수하여 경로 간 차이가 없는 것으로 나타났다(Table 10).

Table 10.

Relative effectiveness analysis of the structural weights Assuming the unconstrained model to be correct: (an≠bn)

7. 가입도 산출을 위한 임계점

(a4:△ADD←△AR_n)−(a3:△AMP←△AR_n)= 0.61^*−1.46^*= −0.85(Table 9)
Direct effects(Total effects-Indirect effects) of path a3=1.46^*−0.16^**=1.30(Table 8, 9)
Direct effects(a3)/Total effects(a4)=1.30/0.61=2.13≒2.00(Table 4, 9)
∴ Critical Point = 1.00 D (hyperopia: AR_f≑0.00 D)

Fig. 1(a) 및 Table 6, 8, 9에서 매개변수 △AR_f를 포함한 경로 a4(△ADD←△AR_n)의 총효과는 0.61^*이며, a3(△AMP←△AR_n)의 총효과는 1.46^*로 유의 하였으며 계수 차는 –0.85이다. 그리고 경로 a4의 간접효과는 −0.17^**이며 경로 a3의 간접효과는 0.16^**로 매개변수 △AR_f의 간접효과는 부(−)와 정(−)의 영향관계에 있다. 이는 AR_n가 가입도에 영향을 미칠 때 매개변수인 AR_f가 부(−)의 영향을 미치고, 반대로 AR_n가 AMP에 영향을 미칠 때 매개변수인 AR_f가 정(+)의 영향을 미친다고 볼 수 있다. 경로 a3와 a4에서 매개변수인 AR_f가 각 경로에 간접효과로 정(+0.16^**)과 부(−0.17^**)의 영향을 미친다는 것이 확인되었다. 따라서 직접효과의 차 –0.85는 Table 3. 조절변수의 빈도분석에서 AR_f의 평균(−0.84±0.02 D)과 근삿값으로 AR_f의 중위수와 최빈값이 –1.00 D의 조건에서 AMP가 평균범위(±2.75≤AMP≤±3.00D)의 경우, AR_f의 기준 범위는 ′−1.00≤AR_f≤−0.85 D′의 조건을 가지게 된다(Table 3, 6, 8, 9)(Fig. 1).

Fig. 1(a) 경로 a3의 총효과(1.46^*)−간접효과(0.16^**)=1.30은 AR_f을 제거한 직접효과로 AR_n 값이라 할 수 있고, 부(−)의 간접효과로 AR_f을 제외한 경로 a4의 총효과 0.61^** 대비 약 2배의 차이(1.31^*/0.61^**=2.14)를 보였다. 이것은 AMP에서 AR_f을 제외한 AR_n 대비해서 매개변수인 AR_f가 부(−)의 간접효과를 포함한 경로 a4의 총효과는 1/2의 값을 가진다는 것이다. 나아가 AR_f의 반응범위(−)가 줄어 AR_n가 2.00 D라 할 때, AR_n의 1/2의 범위인 약 1.00 D에서 가입도에 영향을 미친다는 사실을 확인할 수 있다. 또한 Table 6의 경로 a1(△AR_f←△AR_n)에서 안와 외 자극값이 –3.00 D(divergence: 0.33 m) 조건의 근시모형에서 AR_f가 –1.00 D이면 부(−)의 영향으로 가입도를 결정하는 AR_n의 반응범위 내 임계점은 반대로 1.00 D가 증가하여 2.00 D가 된다.

따라서 외부의 근거리 자극점(stimulus: −0.33 m)에 대한 가입도를 산출하는 기준이 되는 AR_n 범위 내 임계점은 AR_f과 서로 부(−)의 방향으로 이동한다는 사실을 확인할 수 있으며, AR_f의 변화에 따른 가입도를 구하기 위한 AR_n 반응범위 내 가입도 임계점(critical point: C·P) 임상식은 다음과 같다.

∴ Critical Point = 1 − AR_f (myopia: −1.00≤AR_f≤0.00 D, ±1.00≤AMD≤±3.00 D)

안와 외 자극점(0.33~3.00 m)에 대응하는 안와 내 AMP의 범위가 ±3.00 D라 한다면, Table 3 조절변수의 빈도분석에서 양안 AR_f의 평균값은 −0.84 D로 최대 –1.00 D을 넘지 않는 조건에서 근거리 작업시 불편함을 느끼지 못한다. 따라서 통상적으로 임상에서는 –0.25 D의 단위로 처방되기 때문에 안와 내 AR_f가 –0.75 D이라면, AR_f과 AR_n은 서로 부(−)의 영향을 미치기 때문에 AR_n 내 가입도 임계점은 +1.75 D로 원방시 교정 후 AR_n가 +1.75 D에 근접할 경우 가입도는 필요하지 않다(Table 3)(Fig. 1).

이와 같이 AR_f은 AR_n에 부(−)의 영향을 미치고, AR_n은 ADD에 정(+)의 영향을 미치기 때문에 가입도 임계점에도 큰 영향을 미친다. 따라서 AR_f과 관련된 선행연구를 살펴보면 다음과 같다.

대한 안과학회지에 발표된 근시 성인에서 조절마비 전·후와 조절마비제에 따른 굴절 변화 비교(2011)에서 약제안 내 점안 전·후의 MR 굴절 차이를 비교하기 위해서, 제1약제(tropicamide 0.5% & phenylephrine HCI 0.5%) 점안 1시간 후 0.90±0.22 D의 굴절의 차이가 나타났고, 제2약제(cyclopentolate 1.00%) 점안 후 1.15±0.20 D의 차이를 보였다. 그리고 제3약제(제1약제+제2약제)에서는 1.20±.21 D의 차이를 보였다(paired t-test, p<0.05).^[19] 3가지 약제 전·후의 평균값은 1.08 D의 차이를 보인다는 것은 약제마다 상이한 차이가 있지만, Fig. 2에서 AR_f의 보조좌표(AR_f Axis)를 기준으로 평균적으로 –1.00 D의 AR_f을 가지고 있다는 것을 의미한다. 또한 근거리의 조절마비 전·후 검영법의 비교 관찰연구(1987)에서 조절마비제(cycloplegic refraction: CR) 전의 근거리 검영법 검사와 현성굴절 검사(manifest refraction: MR) 대비 차이가 0.97 D의 차이를 보였고, 조절마비 후 0.59 D의 차이를 보였으며 회귀방정식 Y=0.887+0.723χ의 결과를 나타냈다.^[20] 그리고 국내 일반인 229명을 대상으로 한 선행연구(2013)에 의하면, 10~50세 이하의 정상인을 대상으로 1~5군으로 나누어 근시 및 난시를 CR 및 MR 검사에서, 난시는 통계적 유의성이 없었고 근시 도수에서 0.50 D 이상의 차이를 보이는 경우는 73안(16%)으로 근시도가 높은 군일수록 오차율이 높게 나타났다.^[21] 또한 굴절이상에 따른 조절마비 검사 전·후의 시력변화 비교(2006)에서 동일한 굴절교정에서 조절마비제 점안 후에는 산동(CR) 전 보다 근거리는 평균 0.59 logMAR의 감소를 보였고, 원거리와 근거리 시력 및 입체시 모두 전반적으로 저하되었다.^[22] 정시안의 경우 0.69 logMAR로 더 큰 저하를 보였다는 것은, 산동제 점안 후 조절마비상태에서 동공확대에 의한 초점 심도가 낮아 시력의 해상도가 낮은 것도 원인이지만, 근시안에서 조절마비제에 의한 AR_f의 소실로 부(−)의 영향관계에 있는 AR_n가 일시적으로 늘어났기 때문이다. 따라서 단안의 연령의 증가에 따른 안와 내 보상적 변화에 의한 AR_f의 변화에도 불구하고 단 안의 AMP의 변화가 않기 때문에 조절마비제 점안 전·후의 Diopter의 변화값은 본 연구의 조절변수의 빈도분석에서 AR_f의 평균(–0.84±0.02 D)과 유사한 값을 가진다(Table 3).

8. 가입도 산출식

Addition = AR_n−1, (hyperopia: AR_f≑0.00 D, AMP≒AR_n)
Addition = AR_n−C·P, (myopia: −1.00≤AR_f≤0.00 D, ±1.00≤AMP
≤±3.00 D, C·P = 1 − AR_f)
∴ Addition = AR_n − C·P

Fig. 1(a) 근시모형에서 경로 a3의 총효과(1.46^*)에서 간접효과를 제외한 직접효과(1.31^***) 대비 부(−)의 간접효과를 포함한 경로 a4의 총효과(0.61^*) 차이는 약 2.14배이다. 이것은 가입도에 영향을 미치는 AR_n 범위의 1/2지점이다. 원시모형에서 완전교정(AR_f≑0.00 D)한 경우 AR_n은 +2.00 D의 1/2인 +1.00 D지점이 가입도의 임계점이 된다면 AR_n의 범위와 가입도 임계점의 차이가 가입도가 되며 임상식으로 나타내면 ‘Addition=AR_n−1’이 된다.

이를 확장하여 AR_f(−1.00≤AR_f≤0.00 D) 변수가 존재하는 Fig. 1(a)의 근시모형에서 경로 a1(△AR_f←△AR_n)는 부(−)의 영향관계에 있기 때문에 임계값이 변화에 영향을 주기 때문에 임계값의 절대값은 증가된다. 따라서 원시모형의 노안 근용가입도 임상식 ‘Addition=AR_n−1’에서 1 대신 ‘Critical Point = 1 − AR_f (myopia: −1.00≤AR_f≤0.00 D, ±1.00≤AMP≤±3.00 D)’을 적용하면 근시모형의 노안 근용가입도 임상식은 ‘Addition=AR_n-C·P’이 된다.

임상 굴절검사에서 단안 평균 AMP(±2.75≤AMP≤±3.00 D)의 경우 AR_n 범위 내에서 가입도를 결정하는 임계점은 +2.00 D에 근접하며, 연령의 증가에 따른 40대 후반에서는 조절지체의 증가로 AR_n이 증가하거나 이와 연관하여 AMP의 변화로 AR_f가 –0.50 D 이하의 경우 경로 a의 부(−)의 영향으로 임계값이 증가를 하여 +1.50 D로 근거리 작업시 피로감을 느낄 수 있다. Fig. 2.(b) 원시모형안의 경우 완전교정을 위해 AR_f가 시축상 절대좌표의 망막의 원점으로 이동할 경우, AR_n은 부(−)의 영향으로 증가를 하여 AR_n 내에서 가입도 임계점은 +1.00 D로 평균 AMP(±2.75≤AMP≤±3.00 D)의 경우 약 +2.00 D 근접한 임계점을 가지는데 비해서, 원시모형의 경우 +1.00 D 이상의 가입도가 필요하다.

AR_n에 관한 국외 선행연구에서 Morgan(1944)^[23]의 단안조절 반응량의 기대값은 1.25~1.75 D이며, Stine(1960)^[24]과 Milder(1961)^[25]는 근거리의 잔여 근점 조절반응이 +2.00 D 이하에서 정확한 굴절검사가 가능하였고, Cacho(2002)^[26]는 조절용이성 검사에서 가장 적합한 굴절검사는 +2.00 D의 결과를 보였다. 또한 국내 선행연구에는 정상군과 폭주 부족군에서 허성상대조절력 변화량의 비교 연구에서 주시거리 5 m 완전교정의 조건에서 근거리 주시거리(fixation distance: 0.33 m)에서 AR_n은 정상군에서 2.33±0.28 D이고, 폭주 부족군에서 2.16±0.24 D로 AR_n은 0.17 D 차이가 났다. 그리고 저교정(addition: +0.50 D)에서 AR_n은 2.06 D의 결과를 나타냈다.^[27]

근거리 가입도를 이용한 조절과 버전스 반응의 변화에 관한 선행연구에서 0.40 m 자극에 대한 AMP의 평균은 2.03±0.06 D(without +2.00 D), 0.60±0.07 D(with +2.00 D)의 결과를 보더라도, 본 연구에서는 조절지체가 거의 없는 연령 40대 이하의 단안의 AMP가 ±2.75~3.00 D의 조건에서 AR_n가 약 +2.00 D의 경우 원·근방시에 만족스러운 결과를 나타내었던 것은, 안와 외 근점자극(0.33 m)에 대해서 AR_f(−0.75~−1.00 D)을 제외한 나머지(+1.75~+2.00 D)가 AR_n의 반응범위가 되며 AR_n의 반응범위 내 가입도 임계점을 근거로 노안 근용가입도 산출의 기준이 될 수 있다(Fig 1).^[28]