[ Article ]

Journal of Korean Ophthalmic Optics Society - Vol. 28, No. 2, pp.77-82

ISSN: 1226-5012 (Print)

Print publication date 30 Jun 2023

Received 05 Apr 2023 Revised 18 Apr 2023 Accepted 24 Apr 2023

DOI: https://doi.org/10.14479/jkoos.2023.28.2.77

근시안에서 현성과 조절마비 굴절검사에 근거한 예측 안축길이의 비교

김형수¹

; 김상엽²

; 문병연²

; 조현국²

; 유동식²^{, *}

1춘해보건대학교 안경광학과, 교수, 울산 44965
2강원대학교 안경광학과, 교수, 삼척 25949

Comparison of Predicted Axial Lengths Based on Manifest and Cycloplegic Refractions in Myopia

Hyeong-Su Kim¹

; Sang-Yeob Kim²

; Byeong-Yeon Moon²

; Hyun Gug Cho²

; Dong-Sik Yu²^{, *}

1Dept. of Optometry, Choonhae College of Health Sciences, Professor, Ulsan 44965, Korea
2Dept. of Optometry, Kangwon National University, Professor, Samcheok 25949, Korea

Correspondence to: ^*Dong-Sik Yu, TEL: +82-33-540-3415, E-mail: yds@kangwon.ac.kr

초록

목적

근시에 있어서 현성 및 조절마비 하 굴절검사에서 파악된 등가구면굴절력과 각막곡률반경을 이용하여 예측된 안축길이를 실측값과 비교하고자 하였다.

방법

현성 및 조절마비 하에서 자동굴절력계를 사용해 타각적굴절검사 및 각막곡률반경을 측정한 후 안축길이 예측식을 이용하여 안축길이를 계산하고 이를 IOL-Master를 통해 실제 측정한 안축길이와 비교하였다.

결과

현성과 조절마비 굴절검사에서 예측된 안축길이는 각각 25.74±1.28 mm과 25.59±1.27 mm였으며, 측정된 안축길이는 25.39±1.31 mm였다. 현성과 조절마비 굴절검사로부터 예측된 안축길이는 등가구면굴절력과 각각 –0.757과 –0.752로 강한 음의 상관관계를 보였다. 현성과 조절마비 굴절검사로부터 예측과 측정된 안축길이를 비교에서 평균값의 차이는 조절마비 굴절검사로부터 예측된 안축길이의 차이가 0.20 mm로 현성 굴절검사로부터 얻은 차이 0.35 mm보다 정확하였다.

결론

현성 굴절검사보다 더 정확한 조절마비 굴절검사를 기반으로 하는 등가구면굴절력과 각막곡률반경을 이용한 안축길이의 예측이 개인맞춤형 렌즈 설계의 적용에 더 유용한 것으로 본다.

Abstract

Purpose

This study aimed to compare predicted axial length (AL) with the measured AL using the spherical equivalent refractive power and the corneal radius of curvature determined by manifest and cycloplegic refractions in myopia.

Methods

Using an auto-refractometer, objective refraction and corneal radius of curvature were measured under manifest and cycloplegic refractions. The predicted AL was calculated using an AL prediction formula and compared with the measured AL using an IOL-Master.

Results

The predicted AL for manifest and cycloplegic refractions were 25.74±1.28 mm and 25.59±1.27 mm, respectively, and the measured AL was 25.39±1.31 mm. The AL predicted from manifest and cycloplegic refractions showed a strong negative correlation with the spherical equivalent refractive power, -0.757 and -0.752, respectively. The difference between the predicted and measured AL from cycloplegic refraction, the difference between the mean values was 0.20 mm, which was more accurate than the 0.35 mm difference obtained from manifest refraction.

Conclusions

The prediction of the AL using the equivalent spherical power and the corneal radius of curvature based on cycloplegic refraction, which is more accurate than manifest refraction, may be considered more useful for the application of individualized lens designs.

Keywords:

Axial length, Myopia, Manifest refraction, Cycloplegic refraction

키워드:

안축길이, 근시안, 현성 굴절검사, 조절마비 굴절검사

서 론

눈은 각막, 방수, 수정체, 유리체로 구성된 하나의 광학시스템으로 각 구성성분의 굴절력 및 굴절률의 변화가 발생하게 되면 눈 전체의 굴절력 변화로 나타난다. 특히 가장 높은 굴절력을 가진 각막과 수정체의 굴절 시스템의 변화가 나타나게 되면 해당 변화의 대부분이 그대로 눈 전체 굴절력의 변화가 나타나고 안축길이와의 상호관계인 정시화(emmetropization)가 어긋나는 굴절이상도를 보인다.^[1]

근시, 원시, 난시와 같은 굴절 이상도에 맞추어 설계되는 일반적인 안경렌즈의 경우 정점간거리, 경사각, 동공간거리 등의 변수를 표준 적용하여 렌즈를 설계하게 된다.^[2^,^3] 안경 착용자의 굴절이상도 및 착용상태가 표준 적용으로 설계된 렌즈에 근접한다면 큰 문제가 발생하지 않겠지만 차이가 나게 된다면 시각적 불편함을 초래할 수 있다.^[4] 즉, 안경 착용 상태나 눈의 굴절상태에 따라서 실제 눈에 작용하는 굴절력 및 수차에 다양한 변화가 나타나게 된다. 이러한 문제점을 보완하기 위해 프리폼(free form) 형태의 개인맞춤형 안경렌즈가 개발되었고 안경 착용자 개개인의 특성에 따른 다양한 변수를 적용하여 최적의 굴절력을 가지도록 디자인하며 특히 누진굴절력렌즈에서는 주변부에 서 발생하는 불필요한 비점수차를 최적화시켜 시각적 품질, 적응 용이성 등 안경 착용자의 전반적인 만족도를 향상시키고 있다.^[5^,^6] 이러한 렌즈를 디자인하기 위해서는 다양한 변수가 적용되는데 이 중 가장 대표적인 변수는 단안 동공중심간거리, 광학중심점높이, 독서거리, 정점간거리, 경사각, 앞수평면휨각 등이며 프리폼 렌즈 디자인 기술에서는 이러한 변수를 통해 렌즈의 뒷면을 포인트별로 계산하여 각 사용자의 개별 요구에 따라 렌즈를 생산할 수 있습니다.^[7,8]

우리는 앞선 연구^{[9^-11]}에서 개인맞춤형 안경렌즈 디자인에서 안축길이 변수와 이를 측정하기 위한 고가 장비의 필요성을 제기하였고, 임상실무에서 고가 장비 없이 등가구면굴절력과 각막곡률반경을 이용한 안축길이 예측의 정확성을 연구하였다. 그러나 앞서 진행된 연구는 임상현장에 서와 같이 현성 굴절검사에 제한하여 평가하였다. 또한 안축길이 예측식은 등가구면굴절력과 각막곡률반경의 두 변수로만 이루어져 있어 이들의 영향이 크며, 이들 변수의 정확성이 예측된 안축길이의 정확성과 관련이 있으므로 두 변수에 영향을 미치는 굴절검사의 조건이 중요하다. 따라서 굴절검사의 조건 즉, 현성과 조절마비하 굴절검사 차이가 등가구면굴절력과 각막곡률반경의 차이로 연결되고 이것이 결국 안축길이 예측에서 차이를 보일 것으로 생각하였다. 따라서 본 연구의 목적은 현성과 조절마비 굴절검사의 조건에서 얻은 등가구면굴절력과 각막곡률반경를 이용한 안축길이의 예측값과 측정값과 비교 평가하고자 하였다.

대상 및 방법

1. 대상

본 연구에는 9세에서 25세 사이(평균 32.39±10.37세)인 90명(180안)을 대상으로 하였다. 현성 등가구면굴절력은 –4.71±2.55 D였고 조절마비 등가구면굴절력은 –4.34±2.49 D였으며 평균 각막곡률반경은 7.76±0.27 mm였다(Table 1). 안과적 질환이나 수술 경력이 있는 경우와 최대 교정시력이 0.9 미만인 경우에는 대상에서 제외시켰다. 이 연구는 기존의 자료를 이용한 연구로 강원대학교 생명윤리위원회로부터 심사면제 승인(KWNUIRB-2017-12-003)을 받았으며, 헬싱키 선언을 준수하였다.

Table 1.

Demographic and refractive characteristics of myopic subjects

2. 방법

본 데이터는 충북 충주시에 있는 S안과병원의 자료를 이용한 것으로 대상자들을 상대로 자동굴절력계(HRK-7000, Huvitz, Korea)를 이용한 타각적굴절검사를 시행하였으며, 나안시력 측정 후 자동포롭터(DHR-7000, Huvitz, Korea)를 이용하여 교정시력을 측정하였다. 정확한 안축길이는 IOL-Master(IOL Master 500, Zeiss Meditec Inc., Germany)로 측정하였다.

선행 연구^[9^-^11]에서 제시된 여러 안축길이 예측식 중 가장 정확하다고 판별된 Gullstrand-Emsley의 약식 모형안을 이용한 예측식 (1)에 각막곡률반경, 현성 및 조절마비 등가구면굴절력 수치를 대입하여 안축길이를 계산한 후 실제 IOL-Master를 이용해 측정한 안축길이와 비교 분석하였다.

p r e ⁡ A L = (23.90 × C R / 7.80) - (S E × 0.36)

(1)

여기서 preAL은 예측된 안축길이(predicted axial length)이며, CR은 평균각막곡률반경(average corneal radius), SE은 등가구면굴절력(spherical equivalent)이다.

3. 자료 분석

자료의 분석을 위해 SPSS 22.0 통계프로그램의 반복측정 분산분석(repeated ANOVA)을 이용하였으며, 측정 결과의 상관관계를 분석하기 위해 Pearson 상관분석을 시행하였고, 예측된 안축길이와 측정된 안축길이 측정 자료의 일치도를 분석하기 위해 Bland-Altman plot를 사용하였다. 분석 결과 중 유의확률 p<0.05일 때 통계적으로 유의한 차이가 있다고 판단하였다.

결과 및 고찰

예측 및 측정된 안축길이를 비교 분석한 자료는 Table 2에 제시하였으며 현성 굴절검사 결과를 대입하여 계산(예측)된 안축길이는 25.74±1.28 mm였으며 조절마비 굴절검사의 경우 25.59±1.27 mm였고 IOL-Master를 통해 측정된 안축길이는 25.39±1.31 mm로 나타났으며 세 가지 결과는 모두 통계적으로 유의한 차이를 보였다(p<0.001).

Table 2.

Comparison of predicted and measured axial length

Pearson 상관관계에서 현성과 조절마비 굴절검사로부터 예측된 안축길이는 등가구면굴절력과 각각 –0.757과 –0.752로 강한 음의 상관관계를 보였으며, 각막곡률반경은 0.604와 0.619로 뚜렷한 양의 상관관계를 보였다(Table 3). 또한 측정된 안축길이는 현성과 조절마비 굴절검사의 등가구면굴절력과 각각 –0.748과 –0.758로 강한 음의 상관관계를 나타냈고, 각막곡률반경과 0.507의 상관관계를 나타냈다. 그러나 안축길이의 예측값과 측정값의 차이는 각막곡률반경과의 상관관계가 각각 0.3 이하로 약하거나 등가구면굴절력과의 상관성은 유의하지 않았다.

Table 3.

Pearson correlation coefficient for predicted and measured axial length

예측과 측정된 안축길이 모두 각막곡률반경보다 등가구면굴절력과 상관관계가 높았다. 이러한 관계를 통해 안축길이 예측에서 굴절검사의 정확성이 무엇보다 중요하다는 것을 알 수 있다. 특히 측정된 안축길이는 각막곡률반경과 상관관계는 낮으나 조절마비 굴절검사의 등가구면굴절력과 높은 상관성을 보였다. 또한 이러한 관계는 안축길이 예측에서 현성 굴절검사보다 조절마비 굴절검사의 굴절력 평가가 신뢰도를 높이는 중요한 요인으로 본다.

현성과 조절마비 굴절검사로부터 예측과 측정된 안축길이를 비교하기 위한 Bland-Altman 분석에서 평균값의 차이는 조절마비 굴절검사로부터 예측된 안축길이의 차이가 0.20 mm로 현성 굴절검사로부터 얻은 차이 0.35 mm보다 정확하였다(Fig. 1). 이러한 평균 차이는 안구길이의 예측과 실측값의 평균이 클수록 적어지는 경향을 보였다. 또한 조절마비 굴절검사로부터 예측된 안축길이의 일치도 범위는 –0.74 mm~1.15 mm(폭의 범위 1.89 mm)로 현성 굴절검사로부터 예측된 얻은 범위인 –0.60 mm~1.31 mm(폭의 범위 1.91 mm)보다 좁은 범위로 상대적으로 신뢰도가 높았다. Roters 등^[12]은 안축길이를 굴절이상과 각막곡률반경으로부터 예측하는 것과 달리 초자체의 길이와 수정체의 두께로부터 안축길이를 예측하였다. 이는 특히 원추각막의 눈은 수술 후의 굴절이상 결정에서 안축길이의 예측이 중요하기 때문이다. 이 예측은 95% 예측의 한계에서 폭의 범위가 1.65 mm(±0.83 mm)로 본 연구 결과인 1.89 mm와 비슷한 결과이다.

Fig. 1.

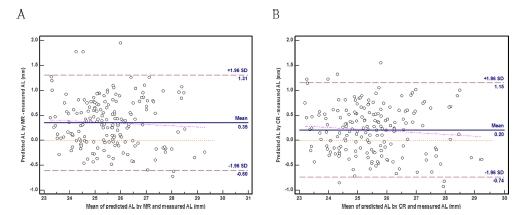
Bland-Altman plots between predicted and measured axial length (AL).A. Comparison between predicted AL by MR and measured AL.B. Comparison between predicted AL by CR and measured AL.Dash-dot-dot lines represent regression lines of differences versus means.

현성과 조절마비 굴절검사에 의한 안구길이의 예측값과 측정값의 차이는 평균과 표준편차에서 각각 0.35±0.49 mm, 0.20±0.48 mm였으며, 예측이 측정보다 큰 경우는 현성 굴절검사에서 129 안으로 71.7%, 조절마비 굴절검사에서 116안으로 64.4%였다(Fig. 2). 구간별로 보면 ±0.50 mm 이내는 현성 굴절검사에서 107안으로 59.4%, 조절마비 굴절검사에서 115안으로 63.9%였으며, ±1.00 mm 이내는 현성과 조절마비 굴절검사에서 각각 168안의 93.3%, 173안의 96.1%였다. 전반적으로 안축길이의 예측값과 측정값의 차이는 현성 굴절검사보다 조절마비 굴절검사를 기준으로 하는 것이 작았다. 결과적으로 조절마비 굴절검사에서의 예측이 정확하다고 볼 수 있다. 조절마비제는 홍채의 괄약근을 마비시켜 홍채 확장을 일으키고 모양체근을 마비시켜 조절 기능이 상실되게 한다. 따라서 조절마비 굴절검사는 조절시스템이 굴절검사에 영향을 주지 않은 조건을 반영한 것으로 현성 굴절검사보다 정확한 검사값을 얻을 수 있다.^[13,14] 그러므로 예측식에 적용하는 등가구면굴절력의 정확성으로 안축길이 예측의 신뢰도가 높은 것으로 여겨진다. 또한, 조절마비 굴절검사에서도 반대쪽 눈을 운무하면 굴절검사가 더 효과적이다는 보고^[15]를 적용한다면 좀 더 신뢰도 높은 안축길이 예측이 될 것으로 판단한다.

Fig. 2.

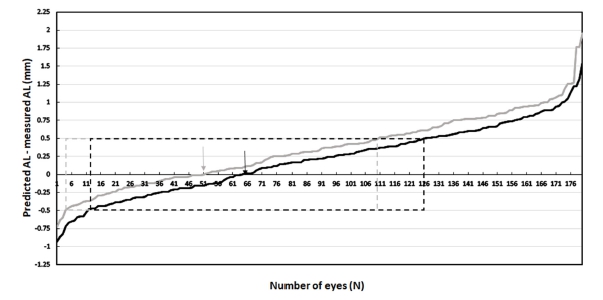
Distribution of differences between predicted and measured axial length (AL).Faint lines and an arrow represent differences by MR.Black lines and an arrow represent differences by CR.

안경렌즈의 설계에는 다양한 변수들이 적용되고 있으며 개인맞춤형 안경렌즈의 경우에는 안경 착용자의 안경 또는 그 안경의 착용 상태에 따라서 그에 맞는 변수들을 적용하여야 하고 특히 누진굴절력렌즈의 경우 이러한 개별변수들을 정확하게 적용하지 않으면 렌즈에 발생하는 주변부 비점수차량이 증가하여 시야의 손실이 발생하게 된다.^[16] 최근에는 이러한 안경 착용 상태에서 발생하는 변수 이외에도 실제 안축길이 측정을 통해 계산된 안구회선점의 위치를 통해 개인맞춤형 안경렌즈로 특히 누진굴절력렌즈를 설계하고 있다.^[17] 안축길이가 긴 경우와 짧은 경우 두 눈의 회선 거리가 달라지게 되고 이로 인해 착용하는 누진굴절력렌즈의 수평 및 수직 방향의 너비도 달리 설계해야 할 것이다.^[18,19] 하지만 현행 한국의 임상 안경원에서 이러한 안축길이를 측정하는 것이 불가능하기 때문에 이러한 변수를 적용하는 것이 어렵다. 따라서 안경사가 임상에서 자주 사용하는 자동굴절력계의 측정 수치인 굴절이상도와 각막곡률반경을 이용하여 안축길이를 예측할 수 있다면 장기적으로 이러한 변수를 누진굴절력렌즈뿐만 아니라 개인맞춤형 안경렌즈의 설계에 손쉽게 적용할 수 있을 것이다.

본 연구에서는 근시에 대한 안축길이 예측값을 분석하였으며 원시와 같은 비정시에 대한 분석이 이루어지지 않았다. 그러나 일반적으로 현성과 조절마비 굴절검사의 차이는 가성근시나 원시에서 더 두드려지는 현상을 보이는 것으로 볼 때 안축길이의 예측값과 실측값의 차이는 조절마비 굴절검사에서 더 정확할 것으로 예측할 수 있다.

결 론

약식 모형안을 근거로 등가구면굴절력과 각막곡률반경을 이용하여 제시한 예측식에 의해 안축길이를 실측값과 비교하였다. 안축길이 예측은 현성 굴절검사보다 조절마비 굴절검사의 등가구면굴절력과 각막곡률반경을 이용한 예측이 더 정확한 것으로 평가되었다. 이러한 결과는 개인 맞춤형 안경렌즈의 설계에서 안축길이 변수를 적용하는데 활용될 것으로 본다.

References

Chinawa EN, Ezeh EI. The distribution of ocular biometrics among patients undergoing cataract surgery. Niger J Ophthalmol. 2018;26(1):40-45. [https://doi.org/10.4103/njo.njo_7_18]
Atchison DA. Spectacle lens design: a review. Appl Opt. 1992;31(19):3579-3585. [https://doi.org/10.1364/AO.31.003579]
Semercİoğlu MG. Basic parameters of lens design. Int J of Health Serv Res and Policy. 2022;7(2):209-220. [https://doi.org/10.33457/ijhsrp.1114224]
Minkwitz G. On the surface astigmatism of a fixed symmetrical aspheric surface. Opt Acta(Lond). 1963;10(3):223-227. [https://doi.org/10.1080/713817794]
Jalie M. Modern spectacle lens design. Clin Exp Optom. 2020;103(1):3-10. [https://doi.org/10.1111/cxo.12930]
Chamorro E, Alonso J, Cleva JM, et al. Free-form lenses: why my patient is not wearing my prescription? JOJ Ophthalmol. 2017;2(1):555577. [https://doi.org/10.19080/JOJO.2017.02.555576]
Pascual E, Gómez-Pedrero JA, Alonso J. Theoretical performance of progressive addition lenses with poorly measured individual parameters. Ophthalmic Physiol Opt. 2023;43(2):244-253. [https://doi.org/10.1111/opo.13088]
Forkel J, Reiniger JL, Muschielok A, et al. Personalized progressive addition lenses: correlation between performance and design. Optom Vis Sci. 2017;94(2):208-218. [https://doi.org/10.1097/OPX.0000000000001016]
Kim HS, Cho HG, Moon BY, et al. Prediction of axial length using schematic eyes in emmetropia. Korean J Vis Sci. 2016;18(2):149-156. [https://doi.org/10.17337/JMBI.2016.18.2.149]
Kim HS, Cho HG, Moon BY, et al. Accuracy of axial length calculation using schematic eyes in ametropia. Korean J Vis Sci. 2016;18(4):455-463. [https://doi.org/10.17337/JMBI.2016.18.4.455]
Kim HS, Yu DS, Cho HG, et al. Comparison of predicted and measured axial length for ophthalmic lens design. PLoS ONE. 2019;14(1):e0210387. [https://doi.org/10.1371/journal.pone.0210387]
Roters S, Hellmich M, Szurman P. Prediction of axial length on the basis of vitreous body length and lens thickness: retrospective echobiometric study. J Cataract Refract Surg. 2002;28(5):853-859. [https://doi.org/10.1016/s0886-3350(01)01169-5]
Elliott DB. Clinical procedures in primary eye care, 5th Ed. Philadelphia: Elsevier, 2021;93-94.
Major E, Dutson T, Moshirfar M. Cycloplegia in children: an optometrist's perspective. Clin Optom (Auckl). 2020;12:129-133. [https://doi.org/10.2147/OPTO.S217645]
Yeotikar NS, Bakaraju RC, P.S. Reddy R, et al. Cycloplegic refraction and non-cycloplegic refraction using contralateral fogging: a comparative study. J Mod Opt. 2007;54(9):1317-1324, [https://doi.org/10.1080/09500340600855346]
Noh JH, Yu DS, Moon BY, et al. Variations in decisions of addition and pupillary distance for progressive addition lenses fitting. J Korean Ophthalmic Opt Soc. 2021;26(4):255-259. [https://doi.org/10.14479/jkoos.2021.26.4.255]
Barcik A, Siedlecki D. Optical performance of the eye with progressive addition lens correction. Optik. 2010;121 (21):1937-1940. [https://doi.org/10.1016/j.ijleo.2009.05.030]
Freedman EG. Interactions between eye and head control signals can account for movement kinematics. Biol Cybern. 2001;84(6):453-462. [https://doi.org/10.1007/PL00007989]
Wu Q, Tang Y, Chen X, et al. Method for evaluating ophthalmic lens based on Eye-Lens-Object optical system. Opt Express. 2019;27(26):37274-37285. [https://doi.org/10.1364/OE.27.037274]