가성근시의 비조절마비 검사방법에 대한 연구

1. 대상

연구 대상자는 경상북도 경산시에 거주하는 만 19~69세 사이 지역 주민 109명을 대상으로 검사를 실시하였고 생명윤리위원회(IRB No: CUIRB-2022-0026)의 연구 허가 후 진행하였다. 검사대상자인 단안 근시 및 가성근시는 연령별로 분리하여 I군(19~39세) 26명, II군(40~49세) 22명, 그리고 III군(50~69세) 20명으로 총 68명을 3그룹으로 구분하여 검사를 진행하였다. 대상자 중 1차 문진을 통해 기저질환이 있는지를 확인하여 백내장 수술 전·후 환자를 제외하였고, 문진이 어려운 경우 검안경을 이용하여 판별하였다. 그리고 조절인자와 관련이 깊은 외사위 군을 제거하기 위해 원거리 1△ 외사위(exophoria), 근거리 6△ 외사위(exophoria) 이상은 연구 대상자에서 제외하였다.^[8]

2. 방법

본 연구는 자동굴절검사기 및 포롭터를 이용한 자각적 굴절검사와 검영기를 이용한 MEM 검사법을 이용하여 외부 자극에 대응하는 안와내 원점과 근점조절반응 그리고 조절반응폭에 의한 굴절교정값인 최적화 모형을 비교 분석하였다.

대상자들의 원거리 객관적 굴절상태를 확인하기 위하여 자동굴절검사기(KR-800, Topcon Japan)로 3회 이상 측정 후 평균값을 사용하여 원거리 타각적 굴절검사를 측정하였고 이를 토대로 원거리 자각적 굴절검사는 포롭터(RT-5100, Nidek, Japan)와 디지털 시력 차트(PO-1001P, Polaopto, Korea)를 이용하였다.

근거리 외부 자극에 대한 조절반응을 확인하기 위해 검영기(no 18245, Wellch Allyn, USA)와 5단 판부렌즈를 이용하여 MEM 검영법을 실시하였다. 검사 값의 일관성을 유지하기 위해 모든 검사는 동일 검사자로 측정되었고 교정굴절력은 구면렌즈 대응치(spherical equivalent)로 비교분석하였다.

가성근시에서 측정 변수 값인 근거리조절반응은 시축에서 망막의 황반부(0.00 D)를 기준으로 각막 방향은 마이너스(−) 굴절력을 가지고 반대 방향을 플러스(+)의 굴절력을 가진 절대좌표를 이용하였고, 원점조절반응은 절대좌표와 –3.00 D의 차인 보조좌표를 사용하였다. 그리고 조절반응폭은 근점조절반응과 원점조절반응 간의 거리라고 할 수 있으며 정상적인 기준치(2.25 D≤ARA≤3.00 D)와의 차이를 비교하여 가성근시와 잠복원시를 판단할 수 있도록 하였다.^[9]

3. 변수의 정의

가성근시의 최적 시력을 위해서는 외부 자극에 대한 망막의 황반부 반응의 폭을 매개 역할로 하여 각 변수들의 상대적 효과와 매개효과에 대한 타당성을 확인하여야 한다. 본 연구는 단안시축에서 황반부중심와를 원점으로 하였으며, 원점조절반응(accommodative response of distance point, ARD)은 각막 방향으로 음(−)의 값을 가지고, 근점조절반응(accommodative response of near point, ARN)은 반대 방향으로 양(+)의 값으로 정의하였다. 원거리 교정굴절력을 구할 때 필요한 변수는 원점조절반응, 근점 조절반응, 조절반응폭(accommodative response amplitude, ARA)으로, 이 세 가지 변수를 이용하여 계산되며 원거리 교정시력 1.0을 기준으로 교정한 상태를 최적 교정상태라고 정의하였다.

본 연구에서 원거리 최적 시력(corrected distance visual acuity, CDVA)은 최대 교정시력이 아닌 원거리 교정시력에 큰 영향을 미치지 않고 근거리에서 피로감을 덜어줄 수 있는 표준 시력 1.0으로 MPMVA(maximum plus to maximum visual acuity)법을 따라 결정하였다.

안구 모형을 구성하는 변수는 근점조절반응, 조절반응폭, 가입도(Addition, ADD) 그리고 교정시력 1.0을 조건으로 하는 원거리 최적 시력으로 구성되었고, 잠복원시와 가성근시의 모형을 구성하는 변수에 대한 정의는 다음과 같다.

근점조절반응(ARN)은 시축선에서 절대값으로 표기를 하며 교정 후 근거리 주시에 대응하는 양(+)의 값을 가지는 조절반응으로 연령의 증가에 따라 절댓값이 커진다. MEM 동적검영은 검영기에 근거리 시표(fixation card)를 부착시킨 후 피검사자가 근거리 0.33 m를 주시하게 하고 판부렌즈 또는 시험렌즈를 +0.25 D 단위로 가입시키면서 동공의 반사광 움직임이 동행에서 역행으로 관찰되는 점을 측정한다. 근거리 0.33 m에서 주시자극에 정상적으로 대응하는 경우의 측정값은 +2.00 D 이내가 대부분이다(Fig. 1).

Fig. 1.

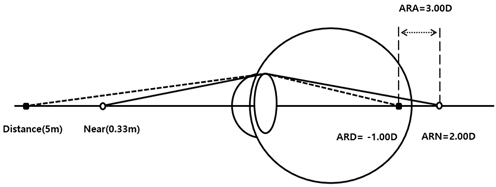
Variables that comprise the normal eye model. Abbreviations: ARD, accommodative response of distance point; ARN, accommodative response of near point; ARA, accommodative response amplitude; CDVA, corrected distance visual acuity

조절반응폭(ARA)은 원거리 교정시력을 1.0으로 교정한 후, 단안에 +3.00 D 착용 전·후의 반응검사를 이용하여 크기를 결정하였다. 즉 피검사자가 근거리 0.33 m를 응시(convergence: +3.00 D)한 후 동일한 거리에서 검사자가 검영기의 확산된 선조광을 이용하여 판부렌즈 또는 시험렌즈로 –0.25 D 증가하면서 역행에서 동행이 나타날 때까지의 크기와 +3.00 D를 제거한 상태에서 원거리를 주시한 후 +0.25 D씩 증가하면서 동행에서 역행이 관찰될 때의 값을 합한 것과 같다.

조절반응폭의 정상수치(±2.25~3.00 D)와 차이가 발생할 경우 근거리 자극(0.33 m)에 대하여 동일하지 않은 반응으로 양안에서 원용 교정시력의 차이가 발생하고 정상수치와 가까운 눈이 단안 시력교정의 기준이 된다.

원점조절반응(ARD)은 조절력에 따라 –1.00 D≤ARD≤0.00 D의 범위 내 있고, 원방시 최적 교정시력인 1.0을 기준으로 잔류하는 굴절 오차를 의미하며 근점조절반응에서 조절반응폭을 뺀 수치가 원점조절반응이 된다.

가입도(ADD)는 교정시력이 1.0을 유지한 상태에서 피검사자가 0.33 m의 근거리를 응시한 후 판부렌즈 또는 시험렌즈로 +0.25 D 증가하면서 역행에서 동행이 나타날 때까지 반응값을 측정한 후 연령에 따른 임곗값을 뺀 수치이다. 임상에서 60세 이상의 완전교정 된 노안의 경우 +1.00 D가 임계치이며 30세 이하의 젊은 나이의 경우 +2.00 D를 임계치로 본다. 평균적으로 +1.50 D를 기준으로 하는 경우가 많다.^[9]

본 연구에서는 0.33 m에서 근거리 조절반응 검사를 실시하여 이론적 조절량은 3.00 D를 기준으로 하였기에 정상안과 청·장년 층의 실제 조절반응 값의 최소와 최댓값의 범위인 1.50~2.00 D를 정상범위로 정의하였다.

일반적으로 근거리 조절반응 검사는 크로스 실린더를 이용한 자각적 근거리 조절반응 검사방법이 임상적으로는 선호하는 편이나 피검자의 반응에 따라 측정값의 변동성이 크므로 본 연구에서 제외하였다.^[10-12] 정시, 근시는 외부자극에 대한 내부 반응이 기본적으로 동일한 선상에서 이루어진다. 단지 정시는 외부 자극에 대응하는 안와 내 시축상에서 황반부를 중심으로 외부의 시각 자극에 대응하는 것을 말한다. 근시는 외부 자극 반응에 대응하는 내부조절반응의 위치가 황반부에서 안내 각막 방향으로 이동하여 반응점의 위치가 다른 것을 말하며 정상적인 조절반응폭의 범위는 ±2.25~3.00 D이다.

가성근시의 원점조절반응은 지속적인 조절로 인하여 소멸된 상태이고, 근점조절반응은 2.00 D 이하인 상태이다. 원점조절반응과 근점조절반응 사이 값을 조절반응폭으로 결정하는데, 이 수치 또한 2.00 D 미만을 나타낸다. 최적 시력을 얻기 위해서 원거리 교정굴절력에 −0.25 D씩 증가시켜 원점조절반응의 수치를 올리면, 이때 조절반응폭 또한 상승하게 된다. (−) 렌즈를 추가하여 조절반응폭이 조정되고 기준값 2.25~3.00 D 범위일 때 최적 시력을 얻을 수 있게 된다(Fig. 2). 조절반응폭에 따른 굴절이상 분류는 다음과 같다.

• Myopia : 2.25 D≤ARA≤ 3.00 D
• Pseudomyopia : ARA≤ 2.00 D

Fig. 2.

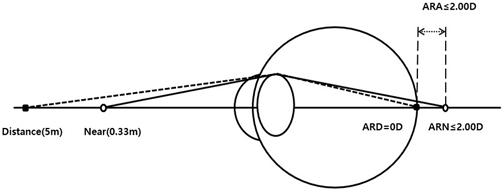
Variables that comprise the eye model for pseudomyopia. Abbreviations: ARD, accommodative response of distance point; ARN, accommodative response of near point; ARA, accommodative response amplitude

근시 및 가성근시의 구분은 단안의 조절반응폭에 의해서 결정된다. 가성근시는 외부 자극에 대응하여 내부 반응의 크기가 작은 것을 의미하고, 최대 교정시력이 근시에 비해서 좋지 못하며 조절반응폭이 2.00 D 이하(ARA≤ 2.00 D)인 것으로 정의하였다. 그리고 근시는 조절반응폭이 2.25 D≤ARA≤ 3.00 D의 범위 내 있기 때문에 원거리 교정시력이 1.0 이상의 값을 가진다.

4. 통계 분석

본 연구는 가성근시모형의 굴절 및 교정시력에 영향을 미치는 조절인자에 대한 정의를 바탕으로 변수를 구하였고 변수 간 영향 관계를 밝혀 모형을 구성하는 매개변수와 변수 간의 모형적합도를 밝히는 데 있다. 변수는 근점조절반응, 조절반응폭, 가입도, 원거리 최적 시력으로 구성되었고 SPSS 22(ver. 22)을 이용하여 각 단안 별로 데이터를 코딩하였다.

변수 간의 회귀모형의 모형적합도 검정을 위해 적합도가 높은 다변량 구조방정식모형으로 경로분석을 이용하여 가성근시 간의 모형적합도를 확인하였다. 원거리 교정시력에 영향을 미치는 독립변수인 근점조절반응과 매개변수인 조절반응폭이 종속변수인 원거리 교정시력에 대한 상대적 효과분석을 위해 공분산 분석으로 각 경로별 직접효과를 확인하여 변수 간의 상관관계를 확인하였다. 그리고 가성근시의 원거리시력 교정효과를 확인하기 위하여 독립표본 T 검정을 통해 분석하였다.

1. 변수들 간의 경로분석 후 모형 확정

최초 설계 모형에서 변수 간의 유의한 영향 관계가 없는 가입도와 관련된 경로를 제거하고 단안 조절반응폭, 근점조절반응 그리고 원거리 교정시력을 주요 변수로 하여 근시안과 가성근시 모형의 적합도(model fit)를 확인한 결과 모두 귀무가설(p>0.05)을 수용하였다(Table 1).

Table 1.

Comparison analysis of the model fits for myopia and pseudomyopia

2. 원거리 교정시력에 대한 연령별 상대적 효과분석

Fig. 3의 대안모형을 이용하여 근시 그리고 가성근시의 그룹별 영향 관계를 확인하였다. Table 2는 근시와 가성 근시에서 각 변수 간 직접효과(direct effect)를 나타내었다.

Fig. 3.

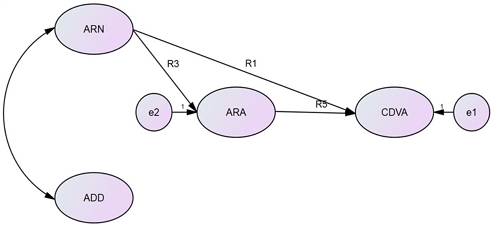
Model (modified model). An alterative model in which the independent variables ARN and the parameter ARA affect the dependent variable CDVA. e1 refers to the difference between the regression equation and the population component

Table 2.

Regression weights (Std, Un Std) of the myopia and pseudomyopia models for direct effects

근시모형 Group I에서 경로 R1(−0.06±0.07, p=0.401)만 음(−)의 효과를 보였지만 통계적으로 유의성은 없었고, 나머지 경로 R3(1.21±0.20, p=0.000), R5(0.09±0.05, p=0.06)에서는 양(+)의 영향 관계에 있었다. G II에서 경로 R1(0.07±0.07, p=0.289)에서 음(Ⅱ)의 영향을 보였지만 통계적으로 유의성은 없었으며, 나머지 경로 R3(0.98±0.33, p=0.003), R5(0.14±0.04, p=0.000)에서는 양(+)의 영향 관계에 있었다. 그리고 나머지 GⅢ에서 경로 R1(−0.10±0.05, p=0.050)에서는 음(−)의 영향 관계에 있었고, R3(0.70±0.25, p=0.005), R5(0.16±0.04, p=0.000)에서 양(+)의 영향 관계로 전 경로에서 유의한 영향 관계를 보여주었다(Table 7). 근시의 경우 모든 그룹에서 근점조절반응이 조절반응폭에 유의한 영향 관계를 보여주었고, 조절반응폭은 원거리 교정시력에 유의한 영향을 미친 것으로 나타났다.

가성근시모형 Group I의 전체 경로 R1(0.17±0.06, p=0.004), R3(0.63±0.14, p=0.000), R5(0.15±0.06, p=0.019)에서 양(+)의 영향 관계를 보여주었고, GroupⅡ에서 경로 R1(0.01±0.09 p=0.985)을 제외한 나머지 경로 R3(0.77±0.17 p=0.000), R5(0.33±0.08 p=0.000)에서 양(+)의 영향 관계를 보여주었다. Group III에서도 경로 R1(0.06±0.08, p=0.469)을 제외한 나머지 경로 R3(0.32±0.19, p=0.092), R5(0.27±0.10, p=0.006)에서 양(+)의 영향 관계에 있었다(Table 2).

가성근시의 경우 조절력이 좋은 Group I에서 단안의 조절반응폭과 근점조절반응(ARN)은 원거리 교정시력에 유의한 영향 관계를 보여주었고, 연령이 증가하면서 원점조절반응이 낮은 Group II, III에는 근점조절반응이 원거리 교정시력에는 직접적인 영향 관계가 없었지만, 조절반응폭에 영향 관계를 보여주었다. 조절반응폭이 원거리 교정시력에 영향을 미쳐 간접적인 영향 관계가 있는 것으로 나타났다.

3. 가성근시의 매개효과 및 간접효과

대안모형인 Fig. 3을 대상으로 Table 1의 계수 값(factor loading)의 유의성을 확인해본 결과 근시 및 가성근시의 매개효과의 결과는 다음과 같다(Table 3). 근시에서는 근점조절반응(ARN)이 매개변수인 조절반응폭(ARA)에 유의한 영향 관계 (0.88±0.15(0.60)^***에 있고, 매개변수도 원거리 교정시력(CDVA)에 유의한 영향 관계(0.02±0.09(0.50)^***에 있다. 그러나, 근점조절반응 및 조절반응폭과 원거리 교정시력 간의 다중회귀식에서 근점조절반응이 원거리 교정시력에 유의한 영향 관계에 있지 않고, 매개변수인 조절반응폭은 완전 매개효과(complete mediation effect)의 결과를 보였다(0.96±0.02(0.02)^***.

Table 3.

Results of tests on the mediating effects of myopia and pseudomyopia

가성근시는 근점조절반응이 매개변수인 조절반응폭에 유의한 영향 관계(0.62±0.09(0.63)^***에 있고, 매개변수도 원거리 교정시력에 유의한 영향 관계(0.28±0.03(0.72)^***에 있으면서 근점조절반응 및 조절반응폭과 원거리 교정시력 간의 다중회귀식에서 모두 유의한 관계(0.23±0.04(0.58)^***를 보여주었다. 근점조절반응의 요인 적재치의 계수가 약해져 있기 때문에 부분 매개효과(partial mediation effect)의 결과를 보여주었다.

근시에서는 조절반응폭은 원거리 교정시력에 유의한 영향 관계를 나타내어 완전 매개효과를 보여주었고, 가성근시에서는 근점조절반응이 조절반응폭에 유의한 영향 관계를 보여주었다. 조절반응폭도 원거리 교정시력에 유의한 영향 관계를 나타내어 부분 매개효과의 영향 관계의 유효성을 확인할 필요성이 있다. Table 4의 결과를 보면 근시 및 가성근시 모두 조절반응폭을 매개변수로 놓고 근점조절반응과 원거리 교정시력 간의 간접효과를 확인한 결과 모두 유의한 결과값을 보여주었다.

Table 4.

Indirect effects (standardized indirect effects) of the unconstrained model (R1≠R5)

근시안에서는 완전 매개효과이고 가성근시에서는 부분매개효과의 영향 관계의 유효성을 확인할 필요성이 있다. 따라서 Table 4의 결과를 보면 근시 및 가성근시 모두 조절반응폭을 매개변수로 놓고 근점조절반응과 원거리 교정시력 간의 간접효과는 유의하였다.

4. 가성근시의 원거리시력 교정효과

양안시 시력교정에서 조절반응폭이 비교적 좋은 기준안에 비해서 가성근시 단안에서는 허용된 굴절량(≤−1.00 D) 만큼의 추가 교정을 통해 원방시의 시력교정을 하여야 할 필요성이 있다. 허용된 굴절교정량이 평균값과 교정 전·후의 대응표본을 이용하여 유의성을 검정한 결과 다음과 같다(Table 5).

Table 5.

Significant effects before and after correction on distance vision in preudomyopia (paired difference T-test)

Table 5의 결과를 보면 가성근시 단안의 원거리 교정시력에 대한 추가 교정의 결과를 보여주었다. 최초 교정시력에서 허용된 추가 굴절교정 범위 내(< −1.00 D) 결정한 것으로 가성근시의 경우 추가적인 굴절 범위의 평균은 (Mean±SD)은 −0.70±0.23 D이고, 원거리시력은 0.46±0.07 상승하였다.

대안모형안의 각 변수의 설정에서 원거리 교정이 필요한 경우 가성근시는 원거리 완전교정굴절력에서 원점조절반응(ARD) 값인 ‘−1.00 D’를 빼고 교정되었다. 가성근시의 경우 현성굴절검사(MR) 대비 –0.30 D 감소하였다.

본 연구는 모형의 경로분석을 이용하여 원거리시력교정에 대한 핵심적인 변수가 무엇인지를 확인하고자 하였다. 일반적으로 원거리 교정시력에 영향을 미치는 요인으로 시표와의 거리, 대비감도, 동공 크기, 굴절이상도, 망막 적응 등을 보고하였고, 본 연구에서는 근점조절반응과 조절반응폭과 같은 안내 조절인자가 원거리 교정시력에 영향을 미치는 것으로 나타났다.^[13] 연령 증가에 따른 변수 간 영향 관계를 살펴보면 가성근시는 연령 증가에 따른 일부 경로에서만 영향 관계가 없었고, 근시의 경우 연령 증가에 관계없이 변수 간의 영향 관계가 유의하였다. 선행 연구에서는 정상인을 대상으로 연령 증가에 따른 변수 간 영향 관계를 확인한 결과 유의성을 나타내어 본 연구와 상이한 결과를 보였는데, 이는 연구 대상이 굴절이상자를 대상으로 하지 않고 정상인을 대상으로 연구를 진행하였기 때문으로 판단된다.^[14]

본 연구의 가성근시모형에서 근점조절반응은 매개변수인 조절반응폭에 유의한 영향 관계를 보여주었고, 매개변수인 조절반응폭도 원거리 교정시력에 유의한 영향 관계에 있으면서, 근점조절반응 및 조절반응폭과 원거리 교정시력 간의 다중회귀식에서 모두 유의한 영향 관계를 보여주었다. 그리고 근점조절반응 및 조절반응폭과 원거리 교정시력 간의 다중회귀식에서 근점조절반응과 조절반응폭 간의 요인 적재치의 계수가 약해져 있으므로 부분 매개효과의 결과를 보여주었다. 결과적으로 근시와 가성근시 모두 조절반응폭을 매개변수로 놓고 간접효과를 검정한 결과 유의성이 있는 것으로 나타났다. 그리고 매개효과와 간접효과의 유의성을 검정한 결과 Table 4의 근시 및 가성근시 모두 독립변수인 근점조절반응과 종속변수인 원거리 교정시력 간에 유의성 있는 결과가 나타났다(Table 3,4).

가성근시의 원거리시력 교정효과 유의성 검정결과 Table 1의 모형적합도를 근거로 Fig. 3의 모형에서 독립변수인 근점조절반응과 매개변수인 조절반응폭 그리고 종속변수인 원거리 교정시력 간의 영향 관계를 살펴보았다. 결과적으로 가성근시모형에서 조절반응폭의 활성화로 안정된 모형인 근시모형으로 변화될 경우 시력교정의 효과는 뛰어날 것으로 보인다(Table 3). 근점조절반응과 조절반응폭은 가성근시의 경우 크기에 비례하여 원거리 교정시력에 도움이 되는 것으로 보여 가성근시의 경우 부분 매개변수인 조절반응폭을 활성화할 경우 원거리시력 교정에 도움이 될 수 있다.