근시용 안경렌즈에서 가장자리 두께와 무게 예측
; Byeong-Yeon Moon2
; Hyun Gug Cho2
; Sang-Yeob Kim2
; Jae-Hyeon Noh2
; Dong-Sik Yu2, *
초록
근시용 안경렌즈에서 다양한 크기와 굴절력에 따른 가장자리 두께와 무게를 예측하고 실측값과 비교하고자 하였다.
1.56, 1.60, 1.67과 1.74의 굴절률과 −2.00 D, −4.00 D, −6.00 D의 굴절력을 갖는 플라스틱 안경렌즈를 대상으로 45 mm, 50 mm와 55 mm의 직경을 갖도록 가공하여 가장자리 두께와 무게를 근사식과 정확한 식에 의해 예측값과 실측값과 비교하였다.
가장자리 두께에서 정확한 식에 의한 예측이 근사식에 의한 예측값보다 컸고 실측값과 유의한 차이를 보이지 않았다. 또한 정확한 식에 의한 예측값과 실측값의 평균 차이가 0.001 mm, 95% 일치도 범위가 −0.15 mm에서 0.14 mm 사이였다. 무게는 두 식에 의한 예측에서 유의한 차이를 보이지 않았고 측정 값과의 비교에서도 유의한 차이를 보이지 않았다.
안경 실무에서 근시용 안경렌즈의 가장자리 두께와 무게를 예측할 필요가 있는 경우 정확한 식에 의한 예측이 실측값을 대체할 수 있을 것이다.
Abstract
This study sought to predict and compare the edge thickness and weight of myopic spectacle lenses based on various sizes and refractive powers.
Plastic spectacle lenses with refractive indices of 1.56, 1.60, 1.67, and 1.74, and refractive powers of −2.00 D, −4.00 D, and −6.00 D were ground to diameters of 45 mm, 50 mm, and 55 mm. Edge thickness and weight were predicted using approximate and accurate equations and were compared with measured values.
The edge thickness predicted by the accurate equation was greater than that predicted by the approximating equation and showed no significant difference from the measured value. In addition, the mean difference between the value predicted using the accurate equation and the measured value was 0.001 mm, with the 95% limits of agreement ranging from −0.15 mm to 0.14 mm. Predictions from both equations did not show a significant difference in weight, and no significant difference was observed in comparison with the measured value.
In optometry practices, accurate equation-based predictions may replace measured values when the edge thickness and weight of myopic spectacle lenses need to be predicted.
Keywords:
Myopic spectacle lenses Edge thickness, Weight, Predictions키워드:
근시용 안경렌즈, 가장자리 두께, 무게, 예측서 론
2050년까지 세계 인구의 49.8%가 근시이고 9.8%가 고도근시로 예측[1]하였을 정도로 근시의 유병률은 증가추세에 있으며 건강 및 사회경제적 문제가 되고 있다. 2019년의 국민건강영양조사[2]에 따르면 우리나라의 근시 유병률은 70.6%, 고도근시의 유병률이 8.0%로 나타났다. 한편, 2023년 대한안경사협회의 발표[3]에 따르면 전국 20세 이상 성인의 73.4%가 안경 및 콘택트렌즈를 사용하고 있고, 콘택트렌즈만 사용하는 2.5%를 제외하면 70.9%가 안경을 사용하는 것으로 볼 때 근시 안경 사용률이 높다고 볼 수 있다.
근시 안경은 교정굴절력과 안경테의 크기나 모양에 따라 안경렌즈의 가장자리 두께와 무게가 다르므로 안경 사용자에게 안경렌즈를 선택하게 할 때 광학적 요소[4-6]와 더불어 두께와 무게와 같은 물리적 요소[7,8]도 중요하다. 이에 관련한 연구로 본 저자들은 근시 안경렌즈를 선택할 때 렌즈의 크기, 굴절력, 굴절률, 비중 및 구면과 비구면 디자인에 따른 안경렌즈의 두께와 무게 변화를 평가하였다.[9] 이 과정에서 시중에 유통되고 있는 다양한 종류의 안경렌즈를 원형 모양으로 가공하여 두께와 무게를 평가하는데 시간과 비용이 적지 않았다. 이러한 적지 않은 투입 자원을 줄이기 위해 렌즈를 가공하지 않고 두께와 무게를 예측할 필요성을 인식하였다. 특히 겉으로 드러나기 쉬운 무테나 반무테에서 근시 렌즈의 두께와 무게를 예측하고 평가하는 것은 무엇보다 중요하다고 본다. 본 연구에서 이러한 점을 고려하여 안경테의 렌즈삽입부크기(eye size)에 맞게 가공하기 전에 두께나 무게를 예측할 수 있다면 안경 사용자나 실무자에게 더 유용한 정보를 제공할 수 있을 것이다.
안경렌즈의 가장자리 두께와 무게 예측은 계산[10-12]이나 웹사이트[13,14]에서 제공하는 계산 시트로 할 수 있으나 현재 유통되고 있는 다양한 렌즈에 대해 예측값과 측정값을 비교한 연구는 없다. 또한 웹사이트에 제공된 계산 시트는 대략적인 예측값이며 어떤 식을 근거하여 제공된 식인지 알 수 없다. 한편 렌즈미터, 구면계, 두께게이지를 이용한 안경렌즈의 굴절률 계산에 관한 연구[15,16]는 두께 예측과 관련된 식을 이용하였으나 무게와 두께 계산과 직접적인 관련은 없었다.
요즘 유통되고 있는 안경렌즈는 대부분 플라스틱 재질의 중굴절(n=1.56) 이상의 렌즈이며, 교정굴절력에 따른 교정 안경렌즈의 선택은 무게나 두께 줄이기 위해 높은 굴절률, 비중이 낮은 소재, 렌즈삽입부크기가 작은 안경테, 비구면 디자인이다. 본 저자들의 이전의 연구[9]는 이러한 상황을 반영하여 안경렌즈의 크기와 굴절력을 변화에 따른 두께와 무게를 평가하였다. 본 연구는 앞선 연구의 후속으로 적절한 안경테에 적용할 근시용 안경렌즈의 가장자리 두께와 무게를 다양한 크기와 굴절력에 따라 예측하고 실측값과 비교하고자 하였다.
재료 및 방법
1. 안경렌즈 선정
안경렌즈는 2023년도 기준으로 국내에 유통되는 렌즈이며 국내 점유율이 20% 이상[17]의 2개 사 제품과 2018년에 출시된 1개 사 제품으로 구성하였다. 수집된 안경렌즈는 플라스틱 렌즈로 굴절률(refractive index, n)이 1.56, 1.60, 1.67과 1.74이며, 굴절력(refractive power)은 −2.00 D, −4.00 D, −6.00 D, 렌즈 디자인은 구면과 비구면 렌즈로 Table 1과 같다.
Optical properties of the selected spectacle lenses
생산되지 않은 안경렌즈는 굴절률 1.56의 –6.00 D인 A사의 구면 디자인 렌즈와 B사의 구면과 비구면 디자인 렌즈, 굴절률 1.74의 –2.00 D인 A와 B사의 비구면 디자인 렌즈를 제외하였고 입수한 렌즈는 렌즈 종류별로 2개씩 총 294개였다.
2. 가장자리 두께와 무게 계산
본 연구는 가공하기 전에 두께나 무게를 가늠할 수 있는 비교적 간단하게 방법으로 구면계를 이용한 평오목렌즈(plano-concave lenses) 기준의 계산식을 이용하여 다양한 종류의 안경렌즈에 대해 예측하고 측정값과 비교하였다.
구면계 공식(spherometer formula)[11,12]은 곡률반경(radius of curvature, r), 새그깊이(sagittal depth, s), 직경 또는 현(chord)의 절반(half-diameter 또는 half-chord, y)의 항으로 r2=(r−s)2 + y2와 같이 표기된다. 여기서 직경이 새그깊이보다 크다(r»s)고 가정할 때 s=y2/2r와 같은 근사식(approximate equation)으로 표시되며, 직경이 크다는 가정을 하지 않을 때 s=r−(r2–y2)1/2로 표시된다. 여기서 렌즈의 중심 두께(center thickness, CT)를 영(0)으로 하고, 새그깊이를 렌즈 가장자리 두께(edge thickness, ET)로, 그리고 곡률반경을 면굴절력(surface power, F)로 대치하면 근사식 (1)과 정확한 식 (2)로 나타낼 수 있으며 이를 이용하여 가장자리 두께를 예측할 수 있다.
| (1) |
| (2) |
여기서 ET1과 ET2은 각각 식 (1)과 (2)에 의해 예측되는 가장자리 두께이며, F은 굴절력, n은 굴절률(refractive index)을 나타낸다.
근사식 (1)에 의해 최종 예측되는 가장자리 두께는 pET1 = ET1 + CT이고, 정확한 식 (2)에 의해 최종 예측되는 가장자리 두께는 pET2 = ET2 + CT이다.
한편 Tang의 연구[18]에서 곡률반경이 새그깊이보다 충분히 크다는 가정 하에 원형 중심의 렌즈 부피(volume, V)는 식 (3)으로 계산하였다. 따라서 계산된 부피에 주어진 비중(specific gravity, Sp)으로 곱하면 렌즈 무게를 예측할 수 있다. 식 (3)에 의해 계산된 부피는 두께로 표현할 수 있으며 식 (4)로 나타낼 수 있다. 따라서 가장자리 두께를 계산하는 근사식 (1)과 정확한 식 (2)를 적용한다면 무게 계산식은 각각 식 (5)와 (6)으로 무게를 예측할 수 있다.
| (3) |
| (4) |
| (5) |
| (6) |
최종 렌즈의 부피는 계산된 부피와 중심 두께에 의해 형성되는 부피(πr2×CT)를 더한 것이다. 여기서 pWeight1과 pWeight2는 각각 근사식 (1)과 정확한 식 (2)를 근간으로 예측되는 렌즈 무게이다.
3. 렌즈 가공 및 가장자리 두께와 무게 측정
굴절력과 광학적 중심을 확인하기 위해서 렌즈미터(VX36, Visionix, Israel)를 이용하였고, 광학적 중심으로부터 원형 모양은 45 mm, 50 mm와 55 mm의 직경 크기가 되도록 자동옥습기(Auto edger Mr Blue Sun & Sport, Essilor, France)를 사용하여 평산각으로 가공하였다. 가공 후 렌즈 크기와 가장자리 두께는 0.01 mm 단위로 측정할 수 있는 디지털 버니어 캘리퍼스(Digital vernier caliper DC200-2, CAS, Korea)를 사용하였고, 중심 두께 또한 0.01 mm 단위로 측정할 수 있는 두께 게이지(Digimatic indicator ID-S1012, Mitutoyo, Japan)를 사용하였다. 렌즈 무게는 0.01 g 단위로 측정할 수 있는 미량저울(Micro weighing scale MWⅡ-H, CAS, Korea)를 사용하였다.
렌즈 두께와 무게는 종류별로 2개의 렌즈에 대해 각각 3회 측정한 다음 2개의 렌즈를 평균하였다.
4. 자료 분석
수집된 자료는 MedCalc 소프트웨어(Version 12.7.7.0, MedCalc Software, Belgium)를 사용하여 분석하였다. 정규분포는 D'Agostino-Pearson 이용하여 검정하였고 두께와 무게의 평균 비교는 반복측정 분산분석(repeated measures ANOVA) 후 Bonferroni 사후 검정하였다. 또한, 평균 비교는 Bland-Altman분석으로 하였다. 통계 분석에서 유의확률(p)이 유의수준(α) 0.05 이하일 때 유의한 것으로 판정하였다.
결과 및 고찰
1. 렌즈의 평균 가장자리 두께와 무게 비교
근사식과 정확한 식에 의해 예측된 평균 가장자리 두께와 무게는 Table 2에 나타내었다. 측정값(ET)과 비교할 때 가장자리 두께는 반복측정 분산분석에서 유의한 차이를 보였다(p<0.001). Bonferroni 사후 분석에서 정확한 식에 예측된 pET2가 근사식에 의해 예측된 pET1보다 컸으나 pET2와 측정값 간에는 유의한 차이를 보이지 않았다. 한편, 예측된 무게는 측정값과 유의한 차이를 보이지 않았다(p=0.144).
Comparison of predicted and measured edge thickness and weight
한편, 렌즈 직경과 굴절력을 기준으로 렌즈의 가장자리 두께와 무게를 반복측정 분산분석의 결과는 Table 3과 같다. 가장자리 두께는 렌즈 직경이 45 mm에서 예측과 측정값 간의 차이는 없었고(p=0.193), 50 mm와 55 mm에서는 유의한 차이를 보였고(각각 p=0.028, p<0.01), Bonferroni 사후 검정에서 pET2가 pET1보다 컸다. 굴절력이 작은 –2.00 D와 큰 –6.00 D에서 예측과 측정값 간의 유의한 차이를 보였고(각각 p<0.01), Bonferroni 사후 검정에서 pET2가 pET1보다 컸으나 –4.00 D에서는 유의한 차이를 보이지 않았다(p=0.111). 위 분석에서 예측된 가장자리 두께는 직경이 클수록 pET2와 pET1간의 차이가 크고 pET2가 pET1보다 측정값과의 차이가 작았다. 굴절력이 크거나 작을 때 pET2와 pET1간의 차이가 나타났으며, 측정값과의 차이는 낮은 굴절력에서는 pET2가 pET1보다 작았으며 높은 굴절력에서는 pET2가 pET1보다 컸다. 렌즈의 무게 예측은 근사식에 의한 예측값인 pWeight1와 정확한 식에 의한 예측값인 pWeight2이 측정값인 Weight과 유의한 차이를 보이지 않았다.
Comparison of predicted and measured edge thickness and weight based on diameter and refractive power
2. 렌즈의 가장자리 두께와 무게의 일치도 분석
근사식과 정확한 식에 의해 예측된 가장자리 두께와 무게를 Bland-Altman 분석을 통해 측정값과의 일치도를 평가하였다. 가장자리 두께의 평균 차이는 pET2가 –0.001 mm으로 pET1의 –0.02 mm보다 작았고, 95% 일치도 범위는 pET2에서 –0.15 mm~0.14 mm로 pET1의 –0.16mm~0.12 mm와 유사하였다(Fig. 1).
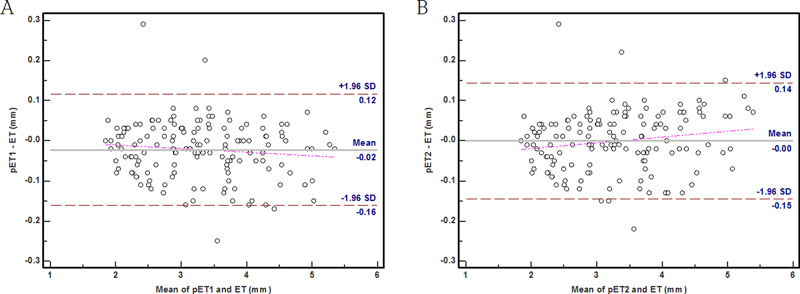
Bland–Altman plots between predicted and measured edge thickness.A. Comparison between predicted edge thickness (pET1) by equation 1 and measured edge thickness (ET).B. Comparison between predicted edge thickness (pET2) by equation 2 and measured edge thickness (ET).The dashed lines represent the upper and lower 95% limits of agreement (mean difference±1.96×standard deviation [SD] of the differences). The solid line represents the mean of the differences. Dash-dot-dot lines represent regression lines of differences versus means.
Bland-Altman 분석에서 가장자리 두께 예측값과 측정값의 평균(x-축)과 평균 차이(y-축)의 회귀식은 pET1에서 y(평균 차이)=0.007–0.009 x(평균)로 유의하지 않았고(p=0.183), pET2에서 y(평균 차이)=0.048+0.014 x(평균)로 유의하였으며(p=0.183), 가장자리 두께에서 예측과 측정값의 평균이 클수록 두 값의 평균 차이가 컸다. 즉 평균이 클수록 예측값이 큰 것으로 평가할 수 있다. 무게의 평균 차이는 pWeight2가 0.01 g으로 pWeight1의 –0.02 g보다 작았고, 95% 일치도 범위는 pWeight2에서 –0.43 g~0.44 g로 pWeight1의 –0.47 g~0.42 g와 유사하였다(Fig. 2). Bland-Altman 분석에서 무게 예측값과 측정값의 평균(x-축)과 평균 차이(y-축)의 회귀식은 pWeight1에서 y(평균 차이)=0.041–0.011 x(평균)로 유의하지 않았고(p=0.314), pWeight2에서도 y(평균 차이)=–0.016+0.004 x(평균)로 유의하지 않은 것(p=0.709)으로 무게에서 예측과 측정값의 평균이 평균 차이에 미치는 영향은 없는 것으로 보인다.
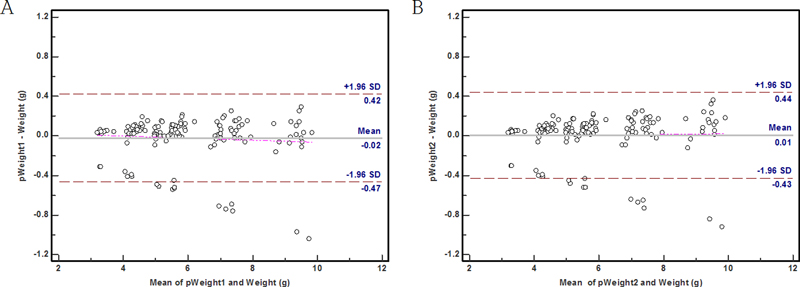
Bland–Altman plots between predicted and measured weight.A. Comparison between predicted weight (pWeight1) by equation 1 and measured weight (Weight).B. Comparison between predicted weight (pWeight2) by equation 2 and measured weight (Weight).Other lines are the same as the footnotes in Fig. 1.
구면과 비구면 디자인 기준으로 가장자리 두께와 무게를 Bland-Altman 분석한 결과는 Table 4와 같다. 구면과 비구면 디자인의 예측된 가장자리 두께는 측정값과의 평균 차이에서 pET1와 pET2 모두 비구면 디자인이 각각 –0.002 mm와 0.02 mm로 작았으나 95% 일치도 범위는 각각 –0.13 mm~0.13 mm, –0.12 mm~0.16 mm로 구면 디자인보다 넓었다. 일치도 범위가 상대적으로 넓으나 그 차이는 0.03 mm와 0.05 mm로 작았다. 구면과 비구면 디자인의 예측된 무게는 측정값과의 평균 차이와 95% 일치도 범위에서 pWeight1과 pWeight2 모두 비구면 디자인이 각각 0.01 mm와 0.04 mm, –0.37 mm~0.40 mm, –0.34 mm~0.42 mm로 작았다.
Bland Altman analysis in edge thickness and weight for spheric and aspheric design
위의 결과는 평오목렌즈 기준으로 근시 렌즈의 가장자리 두께와 무게를 예측하였다. 안경렌즈는 메니스커스 모양으로 가장자리 두께는 중심 두께와 전면과 후면의 새그깊이 차이의 합으로 구성되고,[19] 곡률반경은 전면과 후면의 굴절력으로 치환된다.[15] 위 구성과 치환 조건은 모두 전면과 후면이 구면 디자인일 때 가능할 것이다. 그러나 현재 유통되고 있는 다양한 디자인을 고려하면 적용에 한계가 있다. 본 연구는 이러한 한계를 고려하여 간단한 방법으로 구면계를 이용한 평오목렌즈 기준의 계산식을 이용하여 다양한 종류의 안경렌즈에 대해 예측하고 측정값과 비교하였다.
위의 결과에서 근사식과 정확한 식에 근거하여 근시 안경렌즈의 가장자리 두께와 무게를 예측한 결과 정확한 식에 의한 예측값이 근사식보다 큰 값을 보였다. 이러한 예측값의 차이는 근사식과 정확한 식의 근본 차이에서 비롯된 것으로 근사식이 정확한 식보다 새그깊이의 제곱를 고려하지 않기 때문이다.[20]
가장자리 두께는 측정값과 비교할 때 정확한 식에 의한 예측이 근사식에 의한 예측보다 측정값과 더 일치하였다. 또한 가장자리 두께는 직경이 큰 렌즈에서 예측값과 측정값 간의 차이는 보였다. 이러한 경향은 직경이 클수록 근사식과 정확한 식의 차이 즉 렌즈 직경이 새그깊이보다 크다(r»s)는 가정[20]의 적용 유무에 따른 차이가 더 두드려지기 나타나기 때문으로 해석된다. 그러나 굴절력이 작을 때 예측값 모두 측정값보다 작았고 굴절력 크면 근사식에 의한 예측값이 측정값과 유의한 차이를 보이지 않았으나 굴절력 더 크면 정확한 식에 의한 예측값이 측정값보다 더 컸다. 이러한 경향은 렌즈 굴절력에 따라 다른 전면부의 커브 차이[21]에 따른 결과로 해석된다. 즉 굴절력이 작을수록 전면커브가 크다. 그러나 적용되는 예측식은 전면부 커브를 반영하지 못한 식으로 측정값과 차이를 보이며 굴절력이 클수록 전면커브가 작아 전면커브를 반영하지 못한 식에 근접하는 것으로 생각된다. 렌즈 무게는 직경이나 굴절력 변화에 따라 예측값과 측정값 간의 차이를 보이지 않았다. 이러한 결과는 무게 예측은 가장자리 두께 예측보다 덜 예민한 것으로 평가할 수 있다.
가장자리 두께와 무게 예측은 구면보다 비구면 디자인이 예측값과 측정값의 평균 차이가 적은 것으로 평가된다. 이러한 결과는 전면부 커브를 고려하지 않은 계산식은 전면부 커브가 구면이 아닌 평면을 기준으로 이루어진 식으로서 비구면 렌즈가 구면 렌즈보다 렌즈 가장자리가 얇고 무게가 가벼운 것[22]과 같은 효과를 나타내는 것으로 보인다.
결 론
적절한 안경테에 적용할 근시 안경렌즈에서 가장자리 두께와 무게를 근사식과 정확한 식에 근거하여 예측하고 측정값과 비교하였다. 가장자리 두께는 정확한 식에 의한 예측이 근사식에 의한 예측값보다 컸고 측정값과 비교할 때 일치도가 컸다. 무게는 두 식에 의한 예측에서 유의한 차이를 보이지 않았고 측정값과의 비교에서도 유의한 차이를 보이지 않았다. 따라서 적절한 안경테에 적용할 근시용 안경렌즈의 가장자리 두께와 무게 예측은 정확한 식에 의한 예측이 더 유용할 것이다.
References
-
Holden BA, Fricke TR, Wilson DA, et al. Global prevalence of myopia and high myopia and temporal trends from 2000 through 2050. Ophthalmology. 2016;123(5): 1036-1042.
[https://doi.org/10.1016/j.ophtha.2016.01.006]
-
Han SB, Jang J, Yang HK, et al. Prevalence and risk factors of myopia in adult Korean population: Korea national health and nutrition examination survey 2013-2014 (KNHANES VI). PLoS One. 2019;14(1):e0211204.
[https://doi.org/10.1371/journal.pone.0211204]
- Korean Optometric Association. National survey on the use of glasses and contact lenses in 2023, 2023. https://www.optic.or.kr/pdf/web/viewer.html?file=/data/board/doc/e268c7a056d535fa798f4a94089bfe34.pdf, (29 October 2023).
-
Pillay R, Hansraj R, Rampersad N. Historical development, applications and advances in materials used in spectacle lenses and contact lenses. Clin Optom(Auckl). 2020;12: 157-167.
[https://doi.org/10.2147/OPTO.S257081]
- Jalie M. Ophthalmic lenses and dispensing, 3rd Ed. Oxford: Butterworth-Heinemann, 2008;29-41.
-
Jalie M. Modern spectacle lens design. Clin Exp Optom. 2020;103(1):3-10.
[https://doi.org/10.1111/cxo.12930]
-
Jha GS, Seshadri G, Mohan A, et al. Sulfur containing optical plastics and its ophthalmic lenses applications. EPolymers. 2008;8(1):035.
[https://doi.org/10.1515/epoly.2008.8.1.376]
-
Churms PW. Toric lens volume. Ophthalmic Physiol Opt. 1982;2(2):159-164.
[https://doi.org/10.1111/j.1475-1313.1982.tb00170.x]
- Shim JK, Moon BY, Cho HG, et al. Effect of refractive power and diameter on weight and thickness in spectacle lenses for myopia. J Korean Ophthalmic Opt Soc. 2024; 29(1):9-17.
-
De Faria e Sousa SJ, Ventura L. The exact solution for the centre thickness of spectacle and contact lenses. Ophthalmic Physiol Opt. 1996;16(2):184-186.
[https://doi.org/10.1046/j.1475-1313.1996.95000372.x]
- Meister D. Methods for estimating lens thickness. Optical World. 1997;26(201):1-5. http://static.laramyk.com/wp-content/uploads/2010/05/methods.pdf, (20 December 2023).
- Wakefield KG. Bennett's ophthalmic prescription work, 4th Ed. Oxford: Butterworth-Heinemann, 2002;83-101.
- Wavelength Opto-Electronic (S) Pte Ltd. Weight of a lens, 2023. https://wavelength-oe.com/optical-calculators/lens-weight/, ( 16 February 2023).
- Opticampus. Lens thickness calculation, 2023. http://opticampus.opti.vision/tools/thickness.php, (16 February 2023).
- Mah KC. The compuation of the refractive index in ophthalmic lens using a focimeter, a lens measure and a thickness gauge. J Korea Pub Health Asso. 1990;16(2): 56-60.
-
Simonet P. Theoretical computation of the refractive index in an ophthalmic lens. Optom Vis Sci. 1987;64(5):370-372.
[https://doi.org/10.1097/00006324-198705000-00012]
- Korea Economic Daily. Market share of glasses lens in Korea, 2016. https://www.hankyung.com/article/2016010471481, (2 May 2024).
-
Tang CY. Thickness and weight of lenses for myopia. Ophthalmic Physiol Opt. 1990;10(2):159-167.
[https://doi.org/10.1111/j.1475-1313.1990.tb00970.x]
- Benjamin WJ. Borish's clinical refraction, 2nd Ed. Oxford: Butterworth-Heinemann, 2006;1037-1063.
-
Hwang RY, Gauthier DJ, Wallace D, et al. Refractive changes after descemet stripping endothelial keratoplasty: a simplified mathematical model. Invest Ophthalmol Vis Sci. 2011;52(2):1043-1054.
[https://doi.org/10.1167/iovs.10-5839]
-
Fry GA. Choosing the base curve for an ophthalmic lens. Optom Vis Sci. 1978;55(4):238-248.
[https://doi.org/10.1097/00006324-197804000-00005]
-
Sun WS, Tien CL, Sun CC, et al. Ophthalmic lens design with the optimization of the aspherical coefficients. Opt Eng. 2000;39(4):978-989.
[https://doi.org/10.1117/1.602469]